元件应力分析法是用于详细设计阶段的一种预计方法。 在这个阶段，所使用的元件规格、 数量、 工作应力和环境、 质量系数等应该是已知的，或者根据硬件定义可以确定的， 当使用相同元件时，对它们的失效率因子所做的假设应该是相同的和正确的。 在实际或模拟使用条件下进行鲁棒性测量之前，元件应力分析法是最精确的可靠性预计方法。
物理应力分析是评估电子组件可靠性的一个重要方面。它涉及评估设备的物理封装， 以确保其能够保持结构完整性、 电路互连完整性， 并为电子电路可靠运行提供合适的环境。
注：本文节选自《汽车电子设计：鲁棒性设计》，由机械工业出版社出版
本书特别适合汽车电子工程师、可靠性专家、零部件供应商技术团队及高校师生使用。无论是新能源三电系统开发、智能驾驶域控制器设计，还是车规芯片选型，都能从中获得直接可用的技术工具——如继电器触点匹配表、HALT测试方案模板、参数趋势灰色预测模型等。随书附赠《汽车电子失效模式速查手册》电子版，大幅提升工程问题排查效率。
《汽车电子设计：鲁棒性设计》目录
第1章 失效物理场分析 1
1.1 概述 2
1.1.1 失效物理场的定义和基本原理 2
1.1.2 失效物理场与电子组件鲁棒性的关系 3
1.1.3 失效物理场的分类和常见类型 4
1.1.4 失效的影响 5
1.1.5 失效物理场分析的重要性 6
1.1.6 失效物理场分析的收益 7
1.2 失效物理场的测试方法和技术 8
1.2.1 加速测试与鲁棒性测试 8
1.2.2 失效物理场的模拟与建模技术 9
1.2.3 监测与分析失效物理场的工具和技术 10
1.2.4 失效物理场的分析方法和流程 10
1.3 电子组件失效的物理机制 11
1.3.1 电学失效 12
1.3.2 热学失效 13
1.3.3 机械失效 14
1.3.4 化学失效 15
1.4 电子元件失效的环境相关性分析 18
1.4.1 温度环境 19
1.4.2 湿度 19
1.4.3 氧化和氧环境 21
1.4.4 辐射和电磁干扰 22
1.4.5 振动和机械应力 22
1.5 失效物理场的模型与预测 23
1.5.1 失效物理场的建模 23
1.5.2 失效物理场库 24
1.5.3 失效物理场的预测 24
1.5.4 鲁棒性评估与设计优化 25
1.6 失效物理场的应用和控制策略 26
1.6.1 应用领域 26
1.6.2 控制策略 27
1.7 失效物理场研究的应用 28
1.7.1 失效物理场研究在电子组件设计中的应用 28
1.7.2 失效物理场研究在鲁棒性评估与改进中的应用 29
1.7.3 失效物理场研究在电子制造与维修中的应用 30
1.7.4 失效物理场的控制策略与工程实践 31
1.8 失效物理场分析示例 32
1.8.1 电阻器失效 33
1.8.2 失效模式占失效总比例表 34
1.8.3 失效模式机理分析 35
1.9 PCB 电子组件故障 40
1.9.1 PCB 电子组件故障的6 种类型 40
1.9.2 电子组件故障的分析 41
1.10 常见的电子组件故障 41
1.10.1 机械故障 42
1.10.2 热故障 47
1.10.3 环境故障 47
1.10.4 电应力故障 48
1.10.5 封装故障 52
1.10.6 老化故障 52
1.11 确定元件故障的方法 53
1.11.1 可焊性测试 54
1.11.2 污染测试 55
1.11.3 微切片测试 56
1.11.4 自动X射线检测(AXI) 57
1.11.5 表面成像方法 58
第2 章 元件选型 60
2.1 元件选型过程 60
2.2 元件选型过程不佳的潜在问题 61
2.2.1 成本风险 62
2.2.2 可用性风险 62
2.2.3 不兼容风险 63
2.2.4 未知失效风险 63
2.3 元件选型对鲁棒性的影响 64
2.4 新元件会为可靠的产品性能带来一系列风险 66
2.5 元件选型方法 67
2.6 电阻器选型 67
2.6.1 电阻器选型考虑因素 68
2.6.2 电阻器选型步骤 70
2.6.3 电阻器设计准则 70
2.7 电容器选型 73
2.7.1 电容器选型考虑因素 74
2.7.2 电容器选型步骤 75
2.7.3 电容器设计准则 76
2.8 变压器和电感器选型 77
2.8.1 电感器选型 79
2.8.2 变压器选型 80
2.8.3 电感器和变压器选型步骤 81
2.9 继电器设计 82
2.9.1 继电器的技术参数和选型考虑因素 82
2.9.2 继电器的选型步骤 83
2.9.3 继电器的选型准则 83
2.9.4 继电器使用检查清单 84
2.9.5 继电器的设计方法 86
2.10 开关设计 89
2.10.1 开关的选型考虑因素 90
2.10.2 开关的选型步骤 93
2.10.3 开关的选型准则 93
2.11 晶体和振荡器设计 94
2.11.1 晶体和振荡器的选型考虑因素 95
2.11.2 晶体和振荡器的选型步骤 95
2.11.3 晶体和振荡器的选型准则 96
2.12 光隔离器设计 96
2.12.1 光隔离器的选型考虑因素 97
2.12.2 光隔离器的选型步骤 98
2.12.3 光隔离器的选型准则 98
2.13 断路器和熔断器设计 99
2.13.1 断路器和熔断器的选型考虑因素 99
2.13.2 断路器和熔断器的选型步骤 100
2.13.3 断路器和熔断器的选型准则 101
2.14 插接器设计 102
2.14.1 插接器的选型考虑因素 102
2.14.2 插接器的选型步骤 103
2.14.3 插接器的选型准则 104
2.15 二极管设计 104
2.15.1 二极管的选型考虑因素 105
2.15.2 二极管的选型步骤 105
2.15.3 二极管的选型准则 106
2.16 晶体管设计 108
2.16.1 晶体管的选型考虑因素 109
2.16.2 晶体管的选型步骤 110
2.16.3 晶体管的选型准则 111
2.17 单片微电路和混合微电路设计 112
2.17.1 单片微电路和混合微电路的选型考虑因素 112
2.17.2 单片微电路和混合微电路的选型步骤 113
2.17.3 单片微电路和混合微电路的选型准则 113
第3 章 应力分析 116
3.1 应力与强度概念 117
3.1.1 PSA 的定义和概述 118
3.1.2 PSA 的方法和步骤 119
3.1.3 PSA 的关键参数和指标 119
3.1.4 理想的应力与强度关系 119
3.1.5 实际的应力与强度关系 120
3.1.6 应力曲线和强度曲线分析方法 121
3.1.7 时间的影响 122
3.1.8 PSA 流程 123
3.2 应力与强度分析 124
3.2.1 应力与强度正态假设 124
3.2.2 符号 125
3.2.3 三种情况 125
3.2.4 两个正态分布 128
3.2.5 计算示例 129
3.3 应力类型 130
3.3.1 机械应力分析 130
3.3.2 热应力分析 131
3.3.3 电应力分析 132
3.3.4 化学应力分析 134
3.3.5 环境应力分析 134
3.4 环境和使用因素 135
3.4.1 使用因素的类型 137
3.4.2 产品的任务剖面 138
3.4.3 应力与故障机制的关联 141
3.5 应力和使用因素的表征 142
3.5.1 列表 143
3.5.2 表征 143
3.5.3 注意事项 144
3.6 应力比 145
3.6.1 质量信息 146
3.6.2 应力比 147
3.6.3 示例 147
3.6.4 不同的应力类型导致的失效 148
3.7 应力分析的应用 149
3.7.1 应力分析在元件选型和评估中的应用 149
3.7.2 应力分析在电路板布局和设计中的应用 149
3.7.3 应力分析在封装和连接技术中的应用 150
3.8 PSA 与鲁棒性设计的关系 152
3.8.1 PSA 在鲁棒性设计中的作用与意义 152
3.8.2 PSA 与鲁棒性评估方法的结合 152
3.8.3 PSA 与故障分析和预测的关联 152
3.9 实例研究与案例分析 152
3.9.1 电阻器的应力分析示例 152
3.9.2 电容器的应力分析示例 153
3.9.3 晶体管的应力分析示例 154
3.10 PSA 工具与技术 154
3.10.1 应力测试与分析设备 154
3.10.2 应力仿真与模拟软件 154
3.10.3 应力测量方法与技术 155
第4 章 参数趋势分析 156
4.1 概述 156
4.1.1 参数趋势分析的定义 157
4.1.2 参数趋势分析的作用 158
4.1.3 PTA 和WCCA 的比较 158
4.2 开发元件特性数据库的关键步骤 159
4.2.1 参考数据库来源 160
4.2.2 元件参数趋势分析 160
4.2.3 元件参数趋势量化 161
4.3 参数趋势分析过程 162
4.3.1 确定分析方法 163
4.3.2 获取数据 163
4.3.3 分析计划 164
4.3.4 执行参数分析 165
4.3.5 记录结果 165
4.4 参数趋势分析方法 166
4.5 电容最小值和最大值的计算 167
4.6 元件参数可变性 167
4.7 数值方法 170
4.8 电子元件参数变化趋势分析的应用案例 171
4.8.1 电阻元件参数变化趋势分析 171
4.8.2 电容元件参数变化趋势分析 171
4.8.3 晶体管元件参数变化趋势分析 173
4.8.4 LDO 元件的参数变化趋势分析 177
第5 章 降额设计 179
5.1 定义 180
5.1.1 降额 181
5.1.2 降额方法 182
5.1.3 术语 183
5.1.4 最大推荐工作条件 184
5.1.5 绝对最大额定值 184
5.2 计算条件 185
5.2.1 最坏情况的预期条件 186
5.2.2 温度降额系数 187
5.3 降额等级的划分 188
5.3.1 Ⅰ级降额 189
5.3.2 Ⅱ级降额 191
5.3.3 Ⅲ级降额 193
5.4 降额规则 195
5.4.1 电阻降额规则 195
5.4.2 电容降额规则 196
5.4.3 电感与变压器降额规则 198
5.4.4 晶体管降额规则 199
5.4.5 二极管降额规则 200
5.4.6 集成芯片降额规则 201
5.4.7 光电元件降额规则 203
5.4.8 开关降额规则 203
5.4.9 继电器降额规则 204
5.4.10 插接器降额规则 206
5.4.11 PCB 降额规则 206
5.4.12 振荡器和谐振器降额规则 207
5.4.13 电位器降额规则 208
5.4.14 光学元件降额规则 209
5.4.15 导线与电缆降额规则 210
5.4.16 电机降额规则 211
5.4.17 灯泡降额规则 211
5.4.18 断路器和熔断器降额规则 213
5.4.19 微波管降额规则 214
5.5 降额参考资源 215
5.6 降额过程 216
5.7 降额使用方法 217
5.8 降额和鲁棒性 218
5.9 考虑降额指南的不同方式 219
5.9.1 供应商降额指南 220
5.9.2 行业降额指南 220
5.9.3 过降额或欠降额的影响 221
5.9.4 电压与失效时间的关系 221
5.9.5 另一种绘制降额信息的方法 222
5.10 总结 224
第6 章 最坏情况电路分析 225
6.1 概述 225
6.1.1 最坏情况电路分析的目的 226
6.1.2 最坏情况电路分析的时机 227
6.1.3 最坏情况电路分析的程度 227
6.1.4 谁应该进行最坏情况电路分析/评审 228
6.1.5 利用最坏情况电路分析进行故障分析 228
6.1.6 最坏情况电路分析的降本增效 229
6.1.7 最坏情况电路分析的成本和进度安排 230
6.1.8 常发问题位置及因素 230
6.1.9 电气测试方法和限制 231
6.1.10 进行最坏情况电路分析的能力要求 232
6.2 WCCA 方法论 233
6.2.1 分析方法 233
6.2.2 灵敏度分析 234
6.2.3 参数EVA、RSS、MCA 分析 235
6.2.4 方法和模板 235
6.2.5 公差数据库设置 236
6.2.6 确定关键参数 237
6.2.7 处理定义不明确的公差 237
6.2.8 RSS 计算和应用 238
6.2.9 WCCA 示例: 三端稳压器 239
6.2.10 关联硬件WCCA 结果 243
6.3 最坏情况电路分析的对象与范围 244
6.3.1 最坏情况电路分析的对象 244
6.3.2 最坏情况电路分析的范围 244
6.3.3 最坏情况电路分析的层级 245
6.4 最坏情况电路分析的设计流程 246
6.4.1 最坏情况电路分析准备工作 246
6.4.2 关键电路识别工具 248
6.4.3 确定待分析电路 249
6.4.4 明确电路设计的基本参数 249
6.4.5 电路分割 250
6.4.6 最坏情况电路分析的作用 250
6.4.7 分析结果判别 251
6.5 WCCA 分析方法比较 251
6.6 最坏情况电路分析的前期数据准备工作 252
6.7 建立分析模型 253
6.8 出具最坏情况电路分析报告 254
3.2 应力与强度分析
3.2.1 应力与强度正态假设
在实践中， 实现这种理想情况通常是困难的，并且很少有设计能够做到这种程度， 原因如下。
首先， 工程师很难完全了解和表征产品每个元件的所有应力和所有强度。在设计过程中， 工程师通常依赖于已有的数据、文献研究和经验知识来估计元件的应力和强度。 这些估计值可能存在不确定性，因为它们可能是基于相似元件或相似环境条件的数据， 而不是针对具体设计的实际测试数据。
其次， 产品在使用过程中的应力条件可能会有所变化。 环境条件、 工作负荷、 使用习惯等因素都可能导致应力的变化。这使得设计阶段确定的应力和强度关系可能无法准确预测产品在实际使用中的可靠性。
此外， 由于成本和时间等因素的限制， 设计中可能存在一定的设计余量。这意味着工程师在设计阶段可能会将一些元件的强度设定为较低的值，以确保其在实际使用中不会超过限制。这种设计余量的设置使得应力和强度关系无法完全达到理想情况。
在某些情况下， 由于各种因素，某些元件可能会承受高于其生存能力的应力。 这种情况下， 失效的概率可以通过两条曲线的交点来计算。 这两条曲线分别代表应力和强度的分布。
为了计算应力高于强度的概率，工程师可以通过计算两个曲线之间的面积来求解。 这个面积可以通过进行二重积分来定义。这个二重积分将会考虑到应力和强度的分布函数以及它们之间的关系。
当工程师想象这个面积时，可以将其视为重叠曲线下的一条小的正态曲线。该正态曲线代表了在给定应力和强度条件下失效的概率。
通过对这个面积进行计算， 工程师可以获得应力高于强度的概率。这个概率可以用来评估产品的可靠性，并帮助工程师在设计和工程决策中采取适当的措施来降低失效的风险。
需要注意的是， 这种概率计算是基于统计和概率理论的，它假设应力和强度的分布函数是已知的，并且它们之间的关系是线性的。然而，在实际情况中，这些分布函数可能并不完全已知，并且应力和强度之间的关系可能是非线性的。因此， 在进行概率计算时， 工程师需要考虑到这些因素， 并进行适当的调整和估计。
3.2.2 符号
当工程师表征应力和强度时，通常可以使用概率分布来描述它们的值的位置和变化。
失效概率可以用符号pf表示，其定义为其（Y<X），其中Y是强度的随机变量， X是应力的随机变量。
强度 Y是一个随机变量，其均值（平均值）可以表示为 可以，标准差可以表示为 表以。 强度的分布可以用各种概率分布来描述， 如正态分布、 指数分布等。
应力 X也是一个随机变量， 其均值可以表示为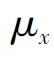
， 标准差可以表示为
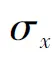。应力的分布也可以用各种概率分布来描述。
安全系数可以定义为强度的均值与应力的均值之间的比值，即安全系数=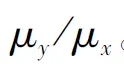
。 安全系数表示了强度相对于应力的保守程度。
安全余量可以定义为强度的均值减去应力的均值， 即安全余量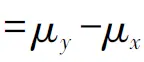
。 安全余量表示了强度与应力之间的余量。
随机变量可以用任何分布来描述， 如正态分布、 指数分布、 韦伯分布等。选择适当的分布函数取决于具体的应用场景和数据特征。
3.2.3 三种情况
在某些情况下， 工程师可能只有应力或强度的估计，或者可能存在不完整的信息。 在这种情况下， 有三种可能的情况可以用于应力和强度的计算。
第一种情况是当工程师只有应力的概率分布函数（PDF）时。在这种情况下， 工程师可以直接使用应力的 PDF来计算失效的概率。 对于固定且已知的强度， 工程师可以将强度与应力进行比较， 并计算强度小于应力的概率。 这个概率就是失效的概率。
第二种情况是当工程师只有强度的概率分布函数（PDF）时。在这种情况下， 工程师可以直接使用强度的 PDF来计算失效的概率。 对于固定且已知的应力， 工程师可以将应力与强度进行比较， 并计算强度小于应力的概率。 这个概率也是失效的概率。
第三种情况是当工程师只有固定且已知的强度，但应力是一个随机变量时。在这种情况下， 工程师需要使用一些微积分方法来计算失效的概率。 工程师需要将应力的 PDF与强度进行卷积， 然后计算强度小于应力的概率。
在这三种情况中， 失效的概率可以通过计算强度小于应力的概率来得到。这可以帮助工程师评估系统或材料的可靠性， 并采取相应的措施来降低失效的风险。图3-5说明了如何通过概率密度函数计算元件在给定强度水平下的失效概率。
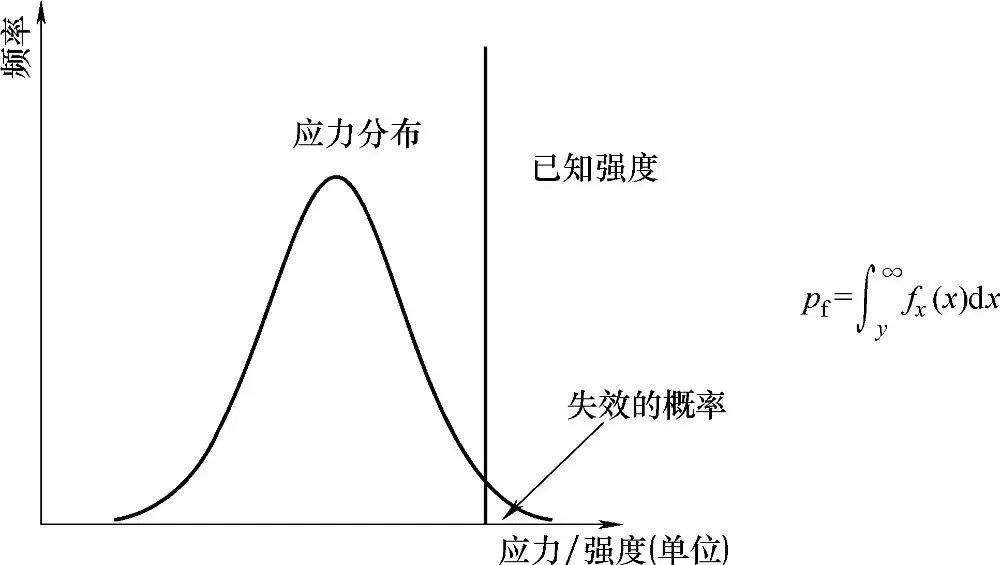
图3-5已知强度和应力随机时的失效概率计算
当应力超过预期强度时， 就会发生失效。 在这种情况下， 工程师可以将应力视为已知， 并且强度是一个随机变量。
在统计学中， 工程师可以用分布函数来描述随机变量的性质。 对于强度这个随机变量Y，工程师可以使用一个概率分布函数来表示它的分布。常见的分布函数有正态分布、 指数分布、 韦伯分布等。
在这种情况下，失效的概率可以表示为应力超过强度分布函数右侧区域的面积。 这个区域代表了强度小于应力的概率， 也就是发生失效的概率。 因此，失效的概率可以通过计算这个面积来得到。
在实际应用中，工程师可能会根据已知数据和统计分析来估计强度的分布函数， 并计算失效的概率。 这可以帮助工程师评估系统或材料的可靠性， 并制定相应的措施来降低失效的风险。
已知固定强度，应力为随机变量：如果应力超过已知的强度，则发生故障。故障概率是应力分布右侧已知强度值下的面积。
已知固定应力，强度为随机变量：如果强度低于已知的应力，则发生故障。故障概率是强度分布左侧已知应力下的面积。
应力和强度都是随机变量： 当应力大于强度时发生故障。故障概率由两个曲线下面积的交集表示， 这是一个单独的分布， 需要近似计算。 当强度低于已知应力时， 就会发生失效。 在这种情况下， 应力和强度都是随机变量，并且工程师可以使用它们的分布函数来描述它们的性质。
图3-6说明了如何通过强度分布的概率密度函数计算元件在给定压力水平下的失效概率。 这里的失效概率是指元件强度小于或等于已知应力的概率， 即元件在该应力下发生失效的可能性。
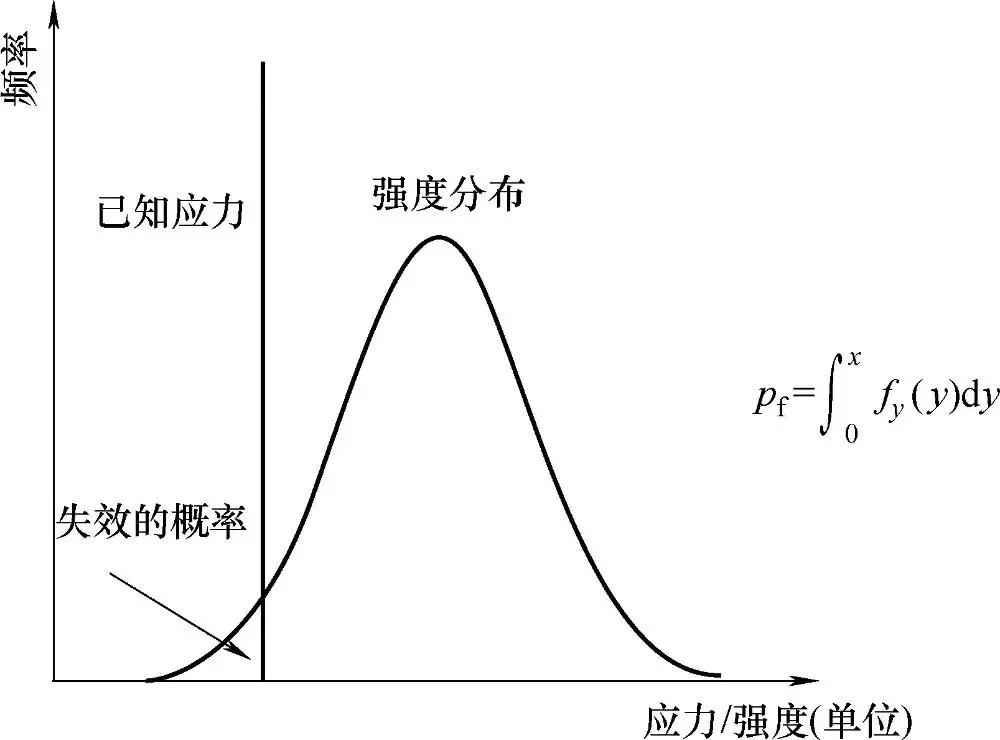
图3-6已知应力和强度随机时的失效概率计算
工程师可以假设应力和强度都服从特定的概率分布， 例如正态分布、指数分布或韦伯分布。这些分布函数可以帮助工程师理解应力和强度的变化范围以及其概率特性。
在这种情况下，失效的概率可以表示为强度小于已知应力分布函数左侧区域的面积。 这个区域代表了强度低于应力的概率， 即发生失效的概率。
通过计算这个面积， 工程师可以得到失效的概率。这个概率可以通过统计方法和已知数据来估计， 从而帮助工程师评估系统或材料的可靠性，并采取相应的措施来降低失效的风险。
在统计学中，失效可以用概率来描述。 工程师可以通过将强度-应力曲线下方的面积作为概率来表示失效的可能性。这个面积代表了在给定条件下材料失效的概率。
在实际应用中， 失效概率往往是一个随机变量， 并且其具有自己的分布。 在下一节中， 工程师可以对失效概率进行近似， 使用适当的统计分布来描述失效概率的特性。
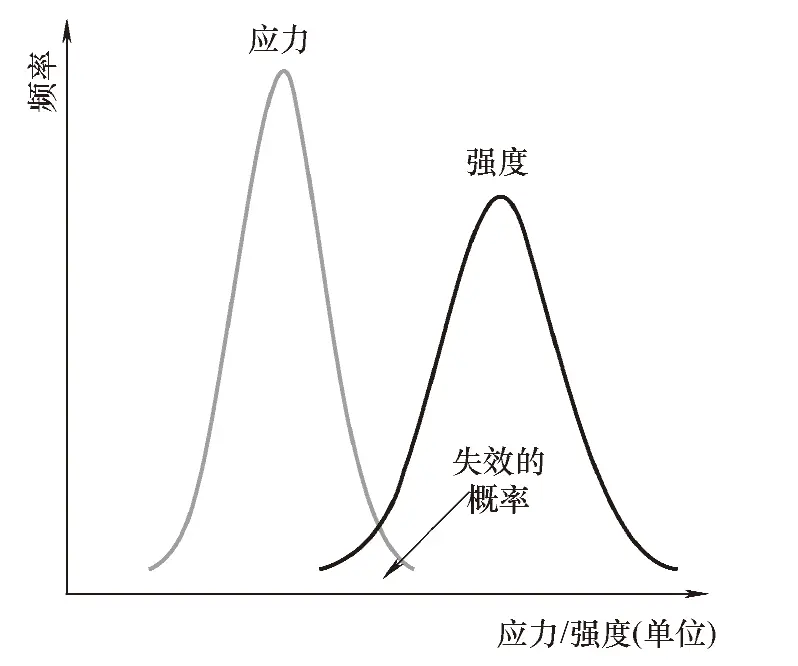
图3-7 应力和强度都随机时的失效概率计算
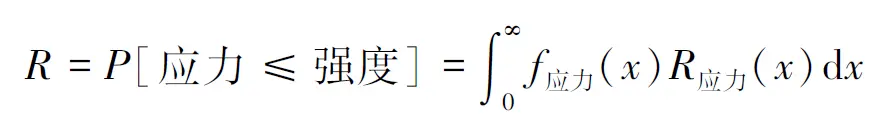
3.2.4 两个正态分布
在某些情况下， 当应力和强度都符合合理的正态分布时， 可以采用差异分布来分析两个分布之间的差异。在这种情况下，工程师可以定义差异变量 变， 表示两个分布的差异， 即 变安以即均， 其中 X和 Y分别为表示应力和强度的变量。
通过分析差异变量D的正态分布特性， 工程师可以对两个分布之间的差异进行推断和比较。 例如， 可以计算差异变量D的置信区间， 从而估计两个分布均值之间的差异范围。 此外， 可以进行假设检验， 检验两个分布之间的差异是否显著。
需要注意的是，差异分布的应用前提是应力和强度都合理地符合正态分布。如果分布不符合正态分布， 或者在特定情况下有其他的分布特性，可能需要使用其他的统计方法来分析差异。此外，还需要注意数据的收集和样本量的大小，以确保分析结果的可靠性和准确性。
安全余量是指在两个分布的均值差异中，强度分布相对于应力分布的差值。它可以用来评估系统或组件的可靠性和安全性。
在这里，Z值是标准正态分布的一个统计量， 通过Z值右侧的面积，工程师可以获得失效概率。这个面积或概率表示了在给定的应力和强度分布下，由于应力超过强度而导致失效的机会。
安全余量的计算和解释可以帮助工程师评估系统或组件的可靠性和安全性。较大的安全余量表示系统或组件更具有可靠性和安全性，因为它们具有更大的阻力来抵抗应力的影响。 相反，较小的安全余量可能意味着系统或组件存在较高的风险和失效概率。
需要注意的是， 安全余量的计算依赖于应力和强度的概率分布。 因此， 在进行安全余量分析时， 需要准确收集和分析应力和强度数据，并了解它们的分布特性。 此外， 还需要考虑其他因素， 例如设计容限和可靠性要求，以便确定安全余量的合理范围。
3.2.5 计算示例
内容简介
本书以汽车电子硬件为背景，层层递迚地引入失效物理场分析、元件选型、应力分析、参数趋势分析、降额设计和最坏情况电路分析等内容。通过这些内容，读者将深入了解如何分析、预测和解决汽车电子系统中的故障和挑战。在每个章节中，还加入了丰富的示例和案例研究，以帮助读者更好地理解和应用所学内容。
本书适合对汽车电子硬件以及技术感兴趣的读者，无论是开发者、设计者、科研工作者还是刚入门的技术人员，均可将本书作为学习参考用书。本书还适合有相关知识背景的从业人员迚行深入学习。
点击以下链接购买
https://mp.weixin.qq.com/s/-sEQYY57f8JMWHo5m5K9Sg
作者简介：高宜国一位在汽车行业从业十多年的资深人士，涉足的领域包括汽车电子器件、汽车电子电路设计、汽车电子鲁棒性设计（DFR）、汽车电子卓越设计（DFX）和汽车电子最坏情况电路分析（WCCA）。作者有个人公众号汽车电子工程知识体系(AEEBOK)，在公众号上将自己的经验和见解整理成文章，内容涵盖了电子器件的选择和应用、电路设计的方法和技巧、测试和可靠性设计的知识点等。希望自己的公众号能够成为广大汽车电子工程师和学习者学习和交流的平台 ，也希望能为汽车行业提供有价值的信息和指导。
本书由机械工业出版社出版，本文经出版方授权发布。
来源：汽车测试网
