路面附着系数估计浅谈
2021-02-28 21:31
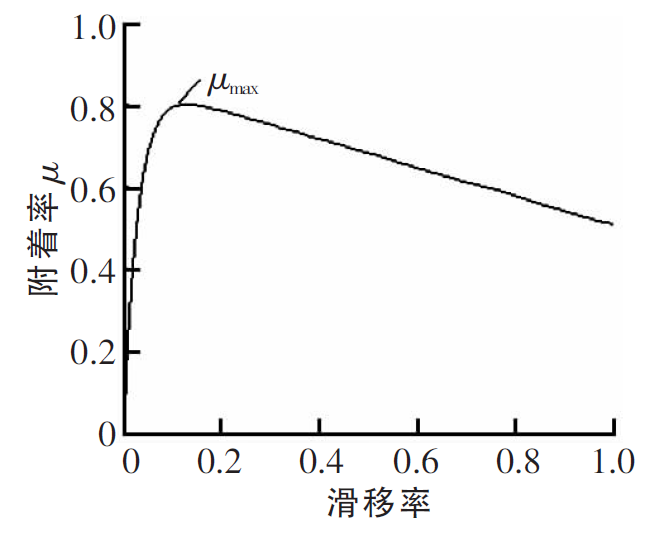
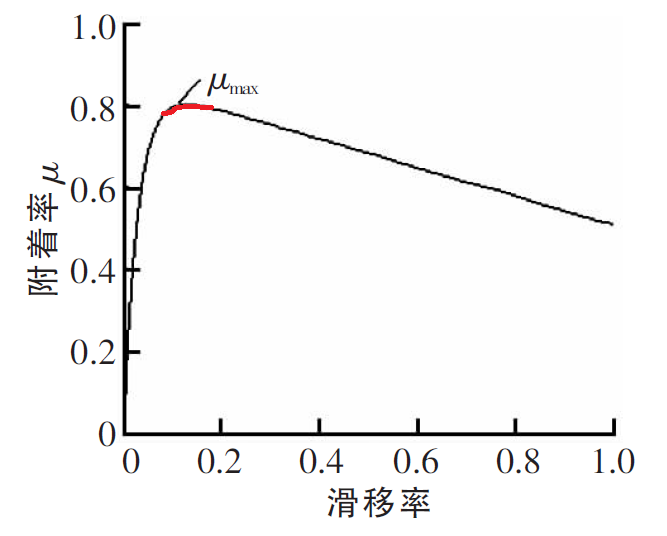
附着率,即轮胎纵向力与垂直载荷的比值,随着滑移率的增大,先增大后减小,如下图(μ-s曲线)所示。一般把某路面下的最大附着率叫做路面附着系数,对应的滑移率在15%左右。 所以,路面附着系数的估计就是最大的附着率的估计。工程上有两种常见的基于μ-s曲线的路面附着系数估计方法:小滑移率范围斜率预估法、大滑移率范围零斜率法。在小滑移范围(0-10%),不同路面附着下的μ-s曲线斜率不同。如果能通过数据拟合出小滑移范围的斜率,即可近似估计出路面附着系数。在大滑移范围(0-20%以上),附着率先增大后减小,所以最大附着率必然对应着零斜率处。如果能实时计算dμ/ds,则dμ/ds接近0附近的附着率即为路面附着系数。以上两种方法均利用了μ-s曲线的相关特性,前者需要较多的数据拟合,但可以做到提前估计,后者只有在大滑移后才能估计,但估计精度更高。
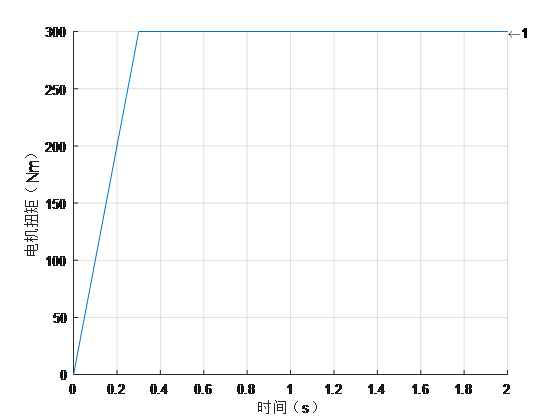
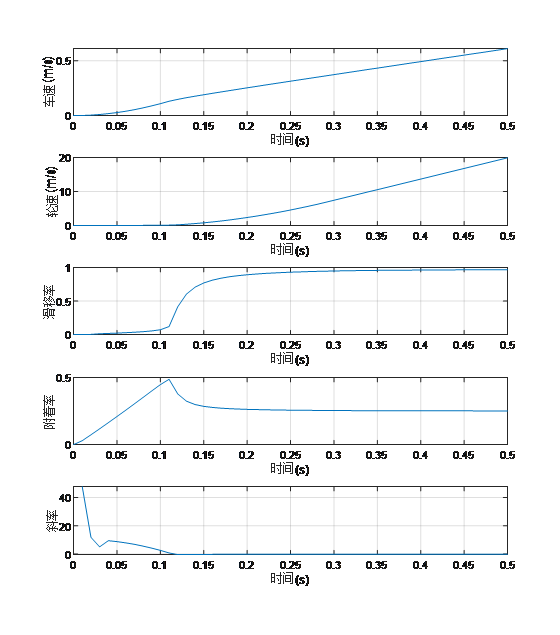
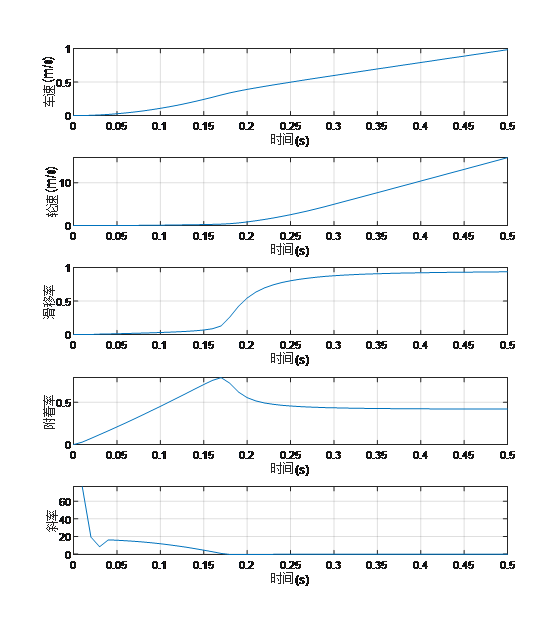
需要说明的是,不管用上面还是其他的路面附着系数方法,都需要尽量准确地计算滑移率、附着率,也就是轮速、车速、地面力等等,这些信号的采集或者估计精度对路面附着系数的估计有着更为重要的影响。搭建一个包含轮胎模型的车辆模型和一个利用车速、轮速、滑移率的估计算法,如下图。车辆模型利用Simulink自带的模块构建,以前的文章已有介绍。估计算法主要是将matlab的滑移率转化为汽车理论中的滑移率,以及根据纵向加速度计算地面力从而得到附着率,再利用滑移率、附着率计算μ-s曲线斜率k。工况1:路面附着系数为0.5,电机驱动力逐渐增大,如下图所示。可以看出,车速逐渐增大,驱动轮转速快速飙升出现滑转,驱动轮滑移率也随之逐渐增大,最终接近于1,车轮附着率先增大至0.5附近,后逐渐减小。我们最为关注的μ-s曲线斜率k在首次接近0附近时也刚好对应着最大附着率0.5。
工况2:路面附着系数为0.8,电机驱动力依然按同样趋势逐渐增大。同样地,车速逐渐增大,驱动轮转速快速飙升出现滑转,驱动轮滑移率也随之逐渐增大,最终接近于1,车轮附着率先增大至0.8附近,后逐渐减小。我们最为关注的μ-s曲线斜率k在首次接近0附近时也刚好对应着最大附着率0.8。
以上,介绍了大滑移率范围零斜率法的路面附着估计方法,并通过仿真进行了验证,基本符合预期,可以作为路面附着估计的一个参考。但是,在实车的操作中,轮速信号的采集延迟及噪声、车速的实时估计误差、地面实际驱动力(制动力)的计算偏差等等,都会对路面附着的估计产生影响,需要根据实车的具体情况做进一步处理。
来源:新能源汽车控制
同类信息