汽车轮肩与轮毂之间气动性能耦合关系分析

前言：汽车行驶的过程中随着车速的提升，气动阻力占总阻力的比值逐渐增大。当汽车以 80km/h 的速度行驶时，其中 60%的功率是用来克服气动阻力的。因此，减小气动阻力是降低动力损耗、节约能源及降低用户使用成本的根本途径。而车轮作为汽车的主要运动部件，在气动阻力方面的影响较大[1]，研究表明，车轮及轮毂占气动阻力的 30%。以往对于汽车车轮的研究，仅限于简单形状的模型，然而，选装车轮的外流场情况复杂，外形几何特征的细微变化会对整个流场有很大的影响[2]。因此，文章基于流体力学的分析方法，通过不同几何特征的车轮对流场变化的影响趋势，分析出了轮胎的轮肩与轮毂之间较强的耦合关系，对改善汽车三维分离流动特性、降低车轮阻力及提高汽车空气动力学性能有重要意义[3]。

1 数值仿真计算

1.1 几何模型的建立

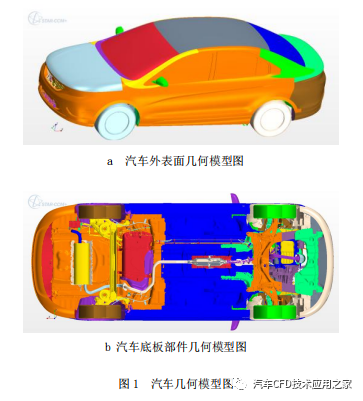
利用 STAR-CCM+软件对汽车模型进行仿真分析，为提高计算结果精度，选取整车全细节几何模型，模型中包括车身外表面、机舱中的全部部件及底板中的全部部件。由于整车外流场仿真计算的区域为整车最外层表面以外的区域，因此乘员舱内的部件模型无需建立，整车几何模型如图 1 所示。

1.2 仿真方案的选定

为深入研究轮肩曲率半径与轮毂之间的耦合关系，明确不同轮肩曲率半径下轮毂开闭及结构变化给气动阻力带来影响程度的规律。文章共设计出8 个组合方案，为不同轮肩曲率半径与轮毂开闭或轮毂结构的组合，具体方案说明如表 1。




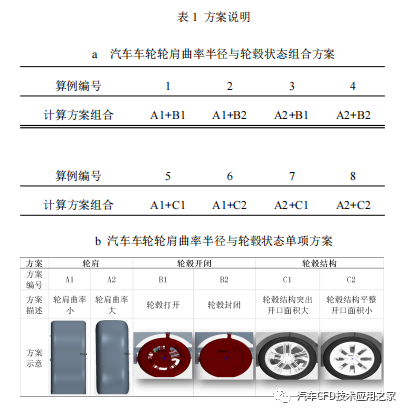
1.3 网格划分及边界条件设置

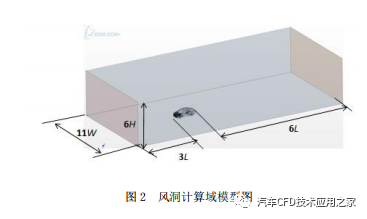
应用 STAR-CCM+中的包面及网格重构技术，对模型进行搭接及网格重构处理，使其生成封闭腔体的面网格。建立风洞计算域模型的具体尺寸，如图 2 所示。在车体外表面与风洞边界之间生成体网格，体网格选用 Trimmer 网格，为更加精准的模拟近壁面的流动情况，在近壁面处划分边界层网格，首层边界层厚度为 0.05mm，层数为 10 层，边界层总厚度为 8 层，体网格数约为 2050 万个左右。


1.4 模型边界条件及介质属性设置

风洞入口边界类型为 Velocity Inlet（速度入口），速度为 100 km/h，出口边界类型为 pressureoutlet（压力出口），压力为 0，车轮转速 100 km/h，地面速度 100km/h，空气密度 1.18415kg/m^3。为准确模拟车辆行驶过程中气流与地面之间的无相对速度关系，地面无速度剪切，特将车身前方地面设置为滑移壁面，其他壁面边界类型为 wall[5]。该计算模型考虑地面运动、车轮转动、换热器（散热器、冷凝器）的阻尼特性及风扇转动对整车外气动性能的影响。

1.5 物理模型模型

采用 SST K-Omega 湍流模型和 All-y+壁面处理方式，三维稳态计算。


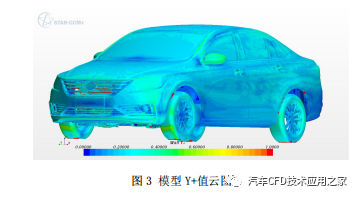
汽车外气动模拟的网格方案应该与所选用的湍流及壁面模型相适应，网格尺寸的适应性可以通过 Y+值来体现。选择 high-y+的壁面模型，要求 Y+的范围是 30-100。选择 low-y+的壁面模型，Y+的值约为 1。该模型中的 Y+值如图 3 所示，大部分区域落在了在 0 到 1 之间。由于稳态方案的 SSTK-Omega 湍流模型在计算 low-y+壁面模型时相对精度较高，因此选用 SST K-Omega 湍流模型[6]。

2 数值仿真结果及分析

通过稳态仿真计算得到上述 8 个组合方案的计算结果，下面分别对不同轮肩曲率半径下的轮毂开闭及轮毂结构方案仿真计算结果进行分析。

2.1 不同轮肩曲率半径下轮毂开闭与气动阻力之间的关系

方案 1、2、3 及 4 为对比不同轮肩曲率半径下轮毂开闭与气动阻力之间关系的方案，四个方案的车轮附近气流分布状况，如图 4 所示。图 4 可以看出，与曲率半径大的轮肩相比，曲率半径小的轮肩其分离点较为靠前，即在轮毂之前，气流已经分离。因此，轮毂是否封闭，对气流分离影响不大，分离点位置无明显变化。相反，曲率半径大的轮肩封闭轮毂后，分离点明显后移。




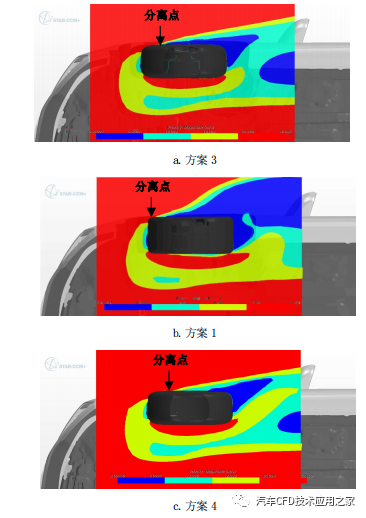
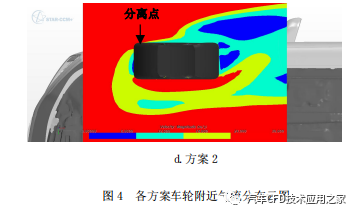
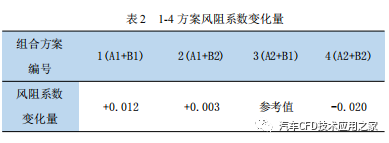
为进一步量化对比不同方案，表 2 中统计出各个方案的风阻系数变化量。以轮肩曲率半径大且轮毂打开的方案 3 为基准参考方案，考察各方案的风阻系数值，仍然能够得到上述规律。图 4a 与图 4b对比，图 4c 与图 4d 对比可以看出轮肩曲率半径大的车轮，气流分离点靠后。图 4a 与图 4c 对比可以看出封闭轮毂后，分离点继续向后移动 90mm，气流贴体性更好，风阻系数（Cd）值下降了 0.02。而图 4b 与图 4d 对比可知，轮肩曲率半径小的车轮，气流分离点靠前，即在轮肩位置气流已经分离，轮毂开闭对分离点位置影响较小，风阻系数（Cd）值变化略小，只下降了 0.009。因此，轮肩曲率半径大的车轮对轮毂开闭敏感性更强。


2.2 不同轮肩曲率半径下轮毂造型结构与气动阻力之间的关系

方案 5、6、7、8 为对比不同轮肩曲率半径下轮毂造型结构与气动阻力之间关系的方案，其风阻系数（Cd）计算结果如表 3 所示，车轮附近气流分布状况如图 5 所示。






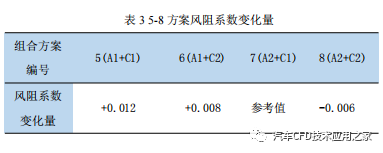
为明确轮毂造型改变所带来的流场改变，以轮肩曲率半径大、轮毂结构突出、开口面积大的方案七为基准参考方案，考察各方案的风阻系数值。由表 3 可知，方案 8 风阻系数较方案 7 下降了 0.006，方案 6 较方案 5 风阻系数下降了 0.004。这主要是由于添加平整、开口面积小的轮毂后，高速气流更加贴体，致使整车风阻系数均有所下降。从图 5a与图 5b 对比可知，轮肩曲率半径大的车轮，分离点位置靠后，添加平整、开口面积小的轮毂后，Cd值下降了 0.006，效果明显。而轮肩曲率半径小的车轮，分离点较为靠前，添加平整、开口面积小的轮毂后，Cd 值只下降了 0.004，说明轮肩曲率半径大的车轮对轮毂结构的敏感性更强。

3 结论

文章以汽车详细模型为基础，运用计算流体力学的方法对不同轮肩曲率半径、轮毂开闭及结构方案进行计算，对比分析得到如下结论：

1）车轮轮毂开闭状态及程度不同直接影响气动阻力系数，在不同曲率半径轮肩的耦合作用下，其影响程度不同；

2）大曲率半径轮肩气流分离点较为靠后，轮毂的开闭及造型状态对气动阻力敏感性较强，因此，大曲率半径轮肩的车轮，在进行轮毂设计时，更要关注轮毂开闭和造型对气动阻力的影响。

来源：汽车空气动力学分会学术年会论文集

作者：付宇