P-S-N曲线是描述材料或结构在特定失效概率下,疲劳寿命与应力水平关系的概率型疲劳特性曲线。如下图
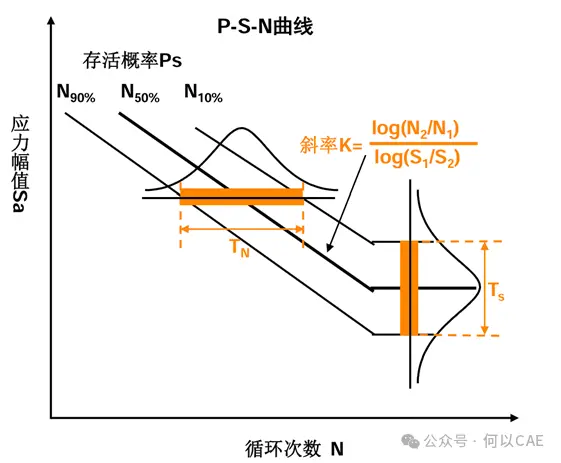
一、几个核心概念
寿命标准差(Slog):衡量寿命数据离散程度。反映数据 “分散度”,值越大离散性越强。
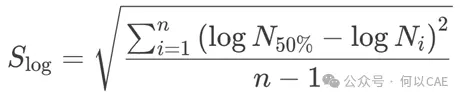
50%存活率寿命(N50%):代表 “半数样本存活到该循环次数”,是最基础的特征寿命。
寿命离散度(TN):直接反映寿命数据的离散程度,值越大离散越明显。
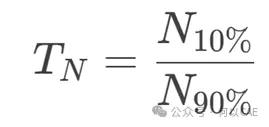
S-N 曲线斜率(m或K):描述“应力幅(S)”和 “循环寿命(N)” 的关系。体现“应力变化对寿命影响的敏感程度”。
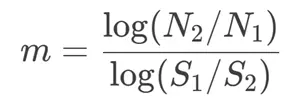
二、P-S-N曲线试验获取
1. 核心原理:
在不同的恒定应力幅水平(S)下,对多组完全相同的试样进行疲劳试验,记录每个试样失效时的循环次数(N)。
2. 应力水平S的选择:
范围:覆盖足够宽的应力范围,从高应力(导致短寿命,10^3-10^4次循环)到接近或低于预估疲劳极限的应力(导致长寿命或无限寿命)。
数量:通常选择 4-8个不同的应力水平。应力间隔在长寿命区(低应力区)应更小,因为此区域寿命对应力变化更敏感。
3. 样本量设计:
每个应力水平下需要的试样数量 n 取决于:目标存活率 P(要求存活率越高,所需试样越多);对寿命分布参数(均值、标准差、形状参数)估计的精度要求;预期的寿命分散性(分散性越大,所需试样越多)。
4. 试验方法选择:
成组法:最常用方法,在每个选定的应力水平 S_i 下,使用 n_i 个试样进行疲劳试验,记录每个试样失效时的循环次数 N_ij (j=1, 2, ..., n_i)。
升降法:主要用于精确测定疲劳极限。 从一个略高于预估疲劳极限的应力开始试验。如果试样在预定循环基数(如1e7)内失效,则下一个试样在降低一级的应力下试验;如果未失效(越出),则下一个试样在提高一级的应力下试验。如此反复,直到完成预定数量的有效试验。
5. 数据处理与统计分析:
将数据按应力水平分组:{S1: [N11, N12, ...,N1n1]}, {S2: [N21, N22, ..., N2n2]}, ..., {Sk: [Nk1, Nk2, ..., Nknk]}。包含越出数据(如标记为 N > 1e7)。
6. 分布拟合与特定存活率下的疲劳寿命计算:
★一个应力水平 S_i做一次分布拟合
威布尔分布:最常用,尤其适用于疲劳寿命数据。使用极大似然估计法(MLE)或最小二乘法拟合形状参数 β_i和尺度参数 η_i (特征寿命)。MLE能更好地处理越出数据。存活率P对应的寿命N_P为
N_P = η_i * [-ln(P)]^(1/β_i)
对数正态分布:对寿命数据取自然对数 ln(N),假设 ln(N) 服从正态分布。拟合均值 μ_i 和标准差 σ_i。存活率 P 对应的寿命 N_P 为
N_P = exp(μ_i + z_P * σ_i),
其中 z_P 是标准正态分布对应存活率 P 的分位数(例如 P=90%, z_P≈1.2816)。
有关这两个分布函数介绍,可翻阅之前的文章哦!!!
7. 绘制 P-S-N 曲线:
1) 横坐标:对数坐标下的循环次数 N(常用 lg N)。
2) 纵坐标:线性坐标下的应力幅 S。
3) 对每个目标存活率 P(如 P=50%, 90%),将不同应力水平S_i下计算得到的N_Pi点画在 S-lgN 图上。
4) 用直线或曲线(如 Basquin方程S^m * N = C或其对数形式)拟合属于同一存活率 P的这些点 (S_i, N_Pi)通常用最小二乘法进行拟合。
5) 最终得到多条曲线,每条曲线代表一个特定的存活率 P。
这样就绘制出了我们文章最前面的曲线图
三、与传统S-N曲线的区别

备注:单一S-N曲线是P-S-N曲线在P=50%时的特例,ncode中默认选项。
作者:何以CAE
来源:何以CAE





