众多从事模态试验的工程师从美国麻省大学洛威尔校区Pete Avitabile教授所著的模态空间系列文章中受益良多。为了能使中国的从业者更准确的理解模态分析基础理论和实践,在与Pete Avitabile教授的多次交流中,德国m+p国际公司北京代表处得到了PeteAvitabile教授在中国大陆唯一翻译发行该系列文章的正式授权,后续的文章将会在全新的公众平台中连载。欢迎您的持续关注。
m+p不仅是产品的制造者、行业技术的推动者,更是知识的分享者。期望我们的努力能够对您的工作有所裨益!

我在X方向上进行激励得到了一些模态结果,而在Y方向进行激励得到了另一些不同的模态结果,我能用一个倾斜的角度对结构进行激励吗?
作者:Pete Avitabile 翻译:倪昊、焦吉祥(德国m+p国际公司)

这个问题很好。这是在使用激振器方式进行模态试验的过程中时常会遇到的问题。在倾斜方向上对结构进行激励当然是可行的,我们唯一要注意的是激励点的位置不能位于结构模态的节点处。我们可以对这个问题进行进一步讨论。
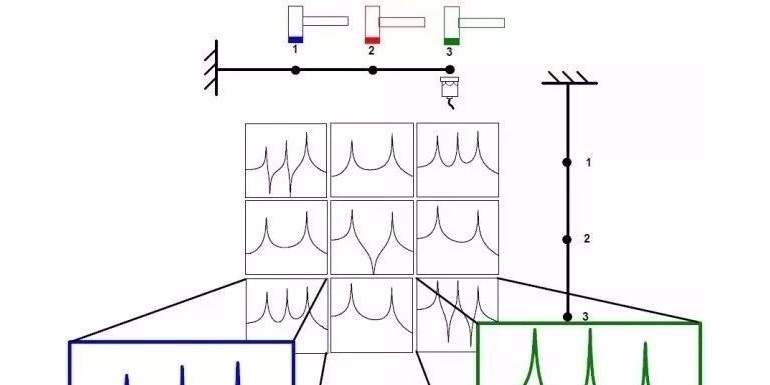
我们先以一个方向性明显的简单结构的模态结果作为例子来讨论。通俗地讲,这个结构在某一阶模态上只在一个方向上有明显的振动,在其它方向上的分量很小或者为零。而另一阶模态会在另一个方向上有明显的振动,其余分量很小或者为零。

图1
如图1中的简单结构,其第一阶模态主要运动方向为水平向,在垂直方向上分量很小,而结构的第二阶模态则主要为垂直方向运动,在水平方向分量很小。我们同样可以看到第三阶与第四阶模态具有相同的趋势。第五阶与第六阶在水平与垂直方向都有运动,但以垂直方向为主。
如果我们查看一个驱动点垂直方向的频响函数(如图2所示),在整个包含六阶模态的测量频带中我们仅能看到两个峰值,而我们知道在这个范围内应该有六个。而我们在水平方向上的测量结果仅能看到四个峰值。在进一步检查结果之后,我们会发现两次测量的结果的前两阶的频率是不同的。

图2
现在我们可以看到,某阶模态并不是在每一个测量结果中都能观察到的。这也就说明如果我们仅选择了两次测量中的其中一个点作为参考点时,我们得到的模态结果是不完整的,但这是为什么呢?
我们现在可以看一下频响函数的表达式:

在此我们将其按3阶模态(举例)展开:

该方程由频响函数中各阶模态的留数(分子)与极点(分母)组成。我们也知道留数与振型(以及归一化因子)是相关的:

因此,频响函数可以留数或振型的形式进行表达,当以振型的方式进行表达时,显而易见,如果某一阶模态振型在参考点为零(或接近于零),该阶模态就不会在频响函数上显现。所以,做好模态试验的技巧之一就是选好参考点,在该参考点上可以看到所有阶的模态。但是,说起来容易,做起来难,尤其是当我们预先不知道结构的振型如何的时候(放马后炮是会容易很多)。

图3
现在我们分别观察前四阶模态。对每阶模态而言其最优的参考点位置是其振型最大值处,但该点的位置在各阶模态上是不同的。因此我们会选择一点,该点在各阶振型上都可以观察到较大的运动。但通常人们总会以一个简单的直角坐标系来考虑这个问题——仅有x,y,z方向。
如果我对结构施加一个与全局坐标系方向呈45度角的力会怎么样呢?该参考点是否可以让我测量得到所有感兴趣的模态?

图4
为了回答这个问题我们依然可以观察频响函数的表达式。当该等式由振型表示的时候,如仅考虑前四阶,我们注意到前四阶模态在该45度角分量上都有响应分量。而这意味着该参考点适用于测量结构的前四阶模态。但进一步观察并考虑第五与第六阶模态,我们很快可以发现该两阶模态在使用该参考点的情况下是无法测得的,这是由于该点为第五阶与第六阶模态的节点。
因此,我们可以选择结构上的任意一点以任意方向作为结构的参考点。唯一的要求是该点在结构的各阶振型上的运动分量都较为明显。如果参考点放置到了结构某阶振型的节点上的话,我们就无法测得该阶模态了。最后要提到的一点是,如果我们要得到有效的“归一化模态振型”,驱动点测量结果是必须的(我们会在以后讨论模态振型归一化)。驱动点的含义为测量响应与激励的位置与方向是相同的,这也适用于与全局坐标系呈角度的参考点。
我希望以上解释能让您理解您可以以任意角度作为您的参考点方向,只要该点不在结构振型的节点上即可。
来源:德国M十P国际公司北京代表处