接上一篇，先来介绍下正态分布函数 ，再介绍几个案例加深对其理解。
1.、正态分布函数
·概率密度函数（PDF）：表示随机变量 X 在点 x 处的概率密度
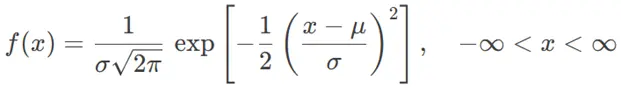
PDF 曲线下方的总面积积分为 1，对应概率的归一性。
·累积分布函数（CDF）：表示X≤x 的累积概率，即 P(X≤x)
2、基于正态分布函数的可靠度分析
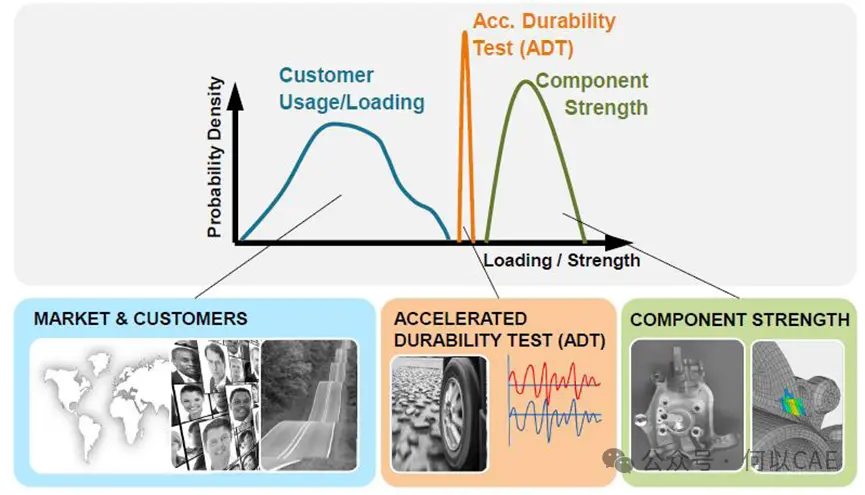
case1：对用户使用载荷进行分析，定义为 X>x0判定为失效，即超过该安全阈值失效：我们假定可靠度要求为 90%（即 R=0.9），需确定阈值 x0
按照正态分布特性，对应分位数z0.9 满足Φ(z0.9)=0.9。查标准正态分布表，z0.9≈1.28。
阈值 x0 的表达式为：
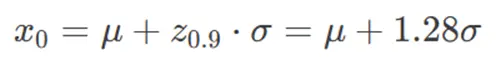
即 设计载荷下限不应低于均值加 1.28 倍标准差，以确保 90% 的可靠性。
case2：对于零件设计强度的要求，定义为 X＜x0判定为失效，即强度低于最小阈值失效，同样的假定可靠度要求为 90%（即 R=0.9），需确定阈值 x0
对应分位数 z0.1 满足Φ(z0.1)=0.1。查标准正态分布表， z0.1≈−1.28。
x0 的表达式为：
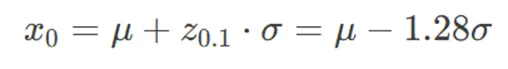
表示 设计最低强度要求为均值减 1.28 倍标准差，以确保 90% 的可靠性。
需要说明的是，实际使用中，若用户载荷存在明显偏态（如重载车辆数据右偏），可能需要改用对数正态分布或其他分布。
而零件强度通常会用Weibull分布描述，威布尔分布通过调整β和η，可拟合多种失效模式（如脆性断裂、疲劳损伤），而正态分布无法描述有下限（如强度不为负）或偏态的数据，同时设计一般需关注强度分布的左尾0.1%分位数（最弱零件），威布尔分布左尾衰减较慢，能更准确地刻画小概率弱强度事件。
3、动力电池随机振动仿真评价
依据标准（如GB 38031、GBT 31467）对试验对象施加频率范围（如5-200Hz）的功率谱密度激励，按预设谱型依次X/Y/Z三轴测试施加随机振动一段时间，考察是否存在失效。
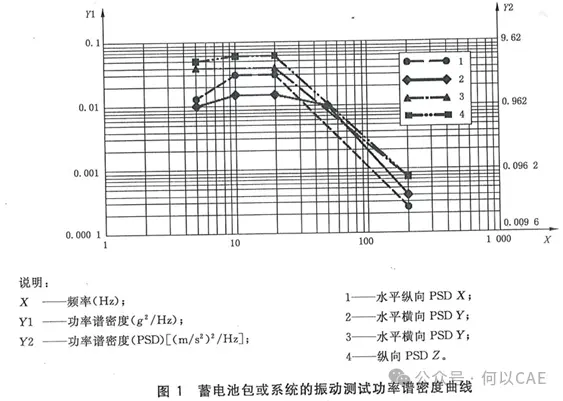
在仿真分析中，因随机振动激励服从正态分布特性，仿真求得的随机响应应力也服从正态分布。可按照正态分布来确定结构可靠程度。
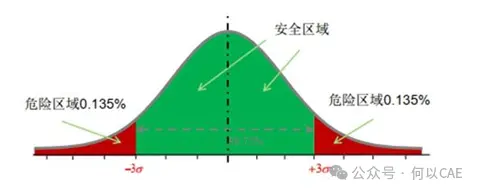
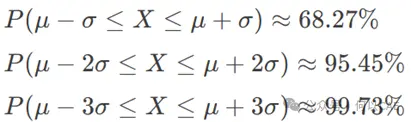
补充一个知识点，RMS与σ的关系
RMS（均方根值）：表示信号的均方根，计算公式为：
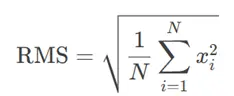
标准差σ：表示数据偏离均值的程度，计算公式为：
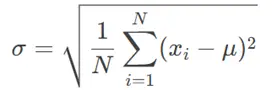可以看出来，当 均值 μ=0 时，RMS与σ数值上相等。
考虑动力电池结构有足够的可靠度，一般按照μ+3σ的原则确定最大应力，用材料屈服或更严苛的疲劳极限应力校核（无限寿命）。具体是应用随机振动分析理论，通过仿真求得单元RMS应力（1σ），由于动力电池包随机振动特点：载荷均值μ为零（RMS=σ），故可直接将RMS应力*3（即3σ）作为零件应力水平。如超出该应力水平，需同时考虑疲劳损伤评估。
作者：何以CAE
来源：何以CAE
