摘要：该论文研究了物理推理中长程系统动力学建模与多任务泛化能力的关键挑战，提出融合哈密顿力学与去噪扩散原理的去噪哈密顿网络（DHN）。尽管现有物理约束模型能学习局部时间状态转移，但其存在两大局限：时间建模局限，仅捕捉相邻时间步关系，无法推演系统级长程相互作用；任务泛化局限，局限于正向模拟，难以处理轨迹修复、参数估计等逆问题。为此，研究者设计了DHN框架，通过三大创新突破上述限制，非局部哈密顿算子、扩散启发的优化机制、全局条件机制。在轨迹预测、参数推断和超分辨率插值三类任务上的实验表明，DHN无须显式构建物理方程即可同时处理正向模拟与逆问题。尤为重要的是，该框架通过神经算子实现了物理约束与数据驱动的深度融合，为科学机器学习开辟了超越局部时间建模的新路径。这些成果不仅推动了物理推理架构的发展，更为复杂系统的多任务学习提供了可扩展的理论基础。
本文译自：《Denoising Hamiltonian Network for Physical Reasoning》
文章来源：arXiv preprint arXiv:2503.07596, 2025.
作者：Congyue Deng, Brandon Y. Feng, Cecilia Garraffo, Alan Garbarz, Robin Walters, William T. Freeman, Leonidas Guibas, Kaiming He
作者单位：麻省理工学院；斯坦福大学
原文链接：https://doi.org/10.48550/arXiv.2503.07596
摘要：用于物理问题的机器学习框架必须能够捕捉并强制实施物理约束，以保持动力系统的结构完整性。许多现有方法通过将物理算子集成到神经网络中来实现这一点。虽然这些方法提供了理论保证，但它们面临两个关键局限：(i)主要建模相邻时间步之间的局部关系，忽略了更长范围或更高层次的物理相互作用；(ii)侧重于正向模拟，而忽略了更广泛的物理推理任务。我们提出了去噪哈密顿网络 (Denoising Hamiltonian Network, DHN)，这是一个新颖的框架，它将哈密顿力学算子推广为更灵活的神经算子。DHN通过去噪机制捕捉非局部时间关系并减轻数值积分误差。DHN 还通过全局条件机制支持多系统建模。我们在三个具有不同输入输出形式的多样化物理推理任务中验证了其有效性和灵活性。
Ⅰ 引言
物理推理，即推断、预测和解释动态系统行为的能力，是科学探究的基础。针对此类挑战设计的机器学习框架，通常被期望超越单纯记忆数据分布，致力于遵守物理定律、考量能量与力的关系，并融入超越纯数据驱动模型的结构化归纳偏置。科学机器学习通过将物理约束直接嵌入神经网络架构（常借助显式构建的物理算子）来解决这一难题。
然而，现有方法存在两大局限：(i)主要学习局部时间更新（预测相邻时间步间的状态转移），未能捕捉长程依赖关系或抽象系统级相互作用；(ii)侧重于正向模拟（从初始条件预测系统演化），基本忽略了超分辨率分析、轨迹修复、稀疏观测参数估计等互补性任务。
为突破这些限制，我们提出去噪哈密顿网络（Denoising Hamiltonian Network, DHN）——将哈密顿力学泛化为神经算子的新型框架。DHN在强制执行物理约束的同时利用神经网络的灵活性，实现三大创新：
首先，DHN将系统状态组视为标记，扩展哈密顿神经算子以捕捉非局部时间关系，使其能整体性推演系统动力学而非孤立时间步。
其次，DHN集成受去噪扩散模型启发的目标函数，通过迭代优化预测轨迹至物理有效状态，减轻数值积分误差。该机制提升长期预测稳定性的同时，保持对不同噪声条件的适应性。利用差异化噪声模式，DHN还支持跨任务场景的灵活训练与推理。
第三，我们引入全局条件机制实现多系统建模。共享的全局潜码编码系统特定属性（如质量、摆长），使DHN能在统一框架下建模异构物理系统，同时解耦底层动力学表征。
为验证DHN的通用性，我们在三大推理任务中测试其性能：(i)轨迹预测与补全，(ii)基于局部观测推断物理参数，(iii)通过渐进式超分辨率插值稀疏轨迹。
综上，本研究推动了超越局部时间关系的物理约束嵌入架构发展，为突破传统正向模拟和状态预测的物理推理开辟了新路径。
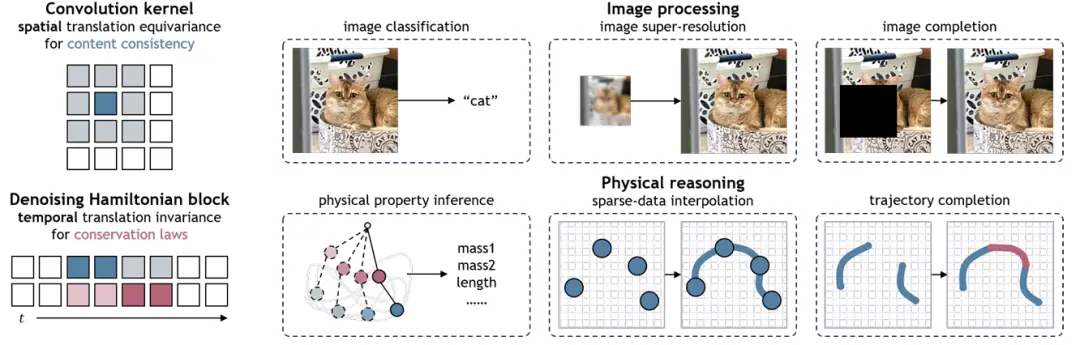
图1 去噪哈密顿网络（DHN）将哈密顿力学推广到神经运算符中。它在利用神经网络灵活性的同时加强物理约束，为物理推理的更广泛应用开辟了道路。
Ⅱ 相关工作
用于物理建模的机器学习方法涵盖了基本运动方程到高维算子学习。我们的工作将Hamilton神经网络（HNN）扩展为一种灵活的、基于序列的范式，可以实现多任务推理和生成条件反射。
哈密顿神经网络（HNNs） 科学机器学习旨在将物理定律嵌入神经网络架构。哈密顿神经网络（HNNs）（Greydanus等，2019）在学习的动力学中强制保持辛结构和能量守恒，启发了多种扩展：拉格朗日神经网络（LNNs）（Cranmer等，2020）、辛ODE网络（Zhong等，2019）以及引入阻尼项的耗散型SymODEN（Zhong等，2020）。研究者还将约束条件纳入HNNs（Finzi等，2020），部分模型可直接从图像序列推断哈密顿动力学（Toth等，2019）。尽管在正向模拟中表现优异，标准HNNs通常每次仅建模单一系统，且依赖均匀步长积分，限制了其在轨迹补全、稀疏数据插值或超分辨率任务中的应用。
物理信息与算子方法 另一类方法将偏微分方程（PDE）约束直接嵌入神经网络（图2示意）。物理信息神经网络（PINNs）（Raissi等，2019）通过PDE约束损失求解正反问题，而傅里叶神经算子（FNOs）（Li等，2020）利用全局傅里叶变换学习函数空间映射。神经ODE（Chen等，2018；Dupont等，2019）通过可学习微分方程参数化连续时间动力学。这些方法虽能有效建模时空PDE，但难以适应不规则采样的离散哈密顿动力学。相比之下，我们的方法通过分块变换直接在离散哈密顿结构上操作，在保持可解释性与稳定性的同时提升灵活性。
系统辨识与多系统建模 从异构物理系统中学习需进行系统辨识，传统方法依赖参数模型（Ljung，1999）或混合PDE约束方法（Raissi等，2019）。哈密顿方法虽通过能量景观隐式编码系统参数，但传统HNNs常需为每个系统单独训练模型。我们提出通过学习潜码的生成式条件机制，使单一模型能泛化至多系统，同时保持哈密顿动力学的归纳偏置。
Ⅲ 方法
A. 动机
我们的目标是设计更通用的神经运算符，既遵循物理约束，又释放神经网络的灵活性和表现力，作为可优化的黑盒函数。我们首先问这样一个问题：除了下一状态预测之外，我们还可以对哪些“物理关系”进行建模？
图2比较了在没有机器学习的情况下建模物理系统的三种经典方法：案例（I）：全局解析解。对于具有规则结构的简单系统，通常直接导出闭合形式的解。案例（II）：偏微分方程+数值积分。在更复杂的设置，其中没有封闭形式的解决方案存在，标准的做法是将系统的动力学表示为PDE，并通过数值方法逐步求解。这种局部积分方法构成了大多数物理约束神经网络设计的基础——这些设计将偏微分方程（PDE）算子编码到网络中，以确保每一步的物理一致性。案例（Ⅲ）：直接全局关系。在某些复杂系统中（例如，没有耗散力的纯保守系统），时间上相距很远的状态可以通过全局守恒定律（例如，能量守恒）直接联系起来。这类似于高中物理问题：人们可以仅从初始条件计算物体在某个位置的速度，而不需要求解完整的轨迹。虽然这比基于偏微分方程的方法更不通用，但它提出了一个有希望的途径：在黑盒神经网络中利用全局物理原理可以将这种技术扩展到更复杂的现实世界动力系统，而不仅仅是简单的教科书问题
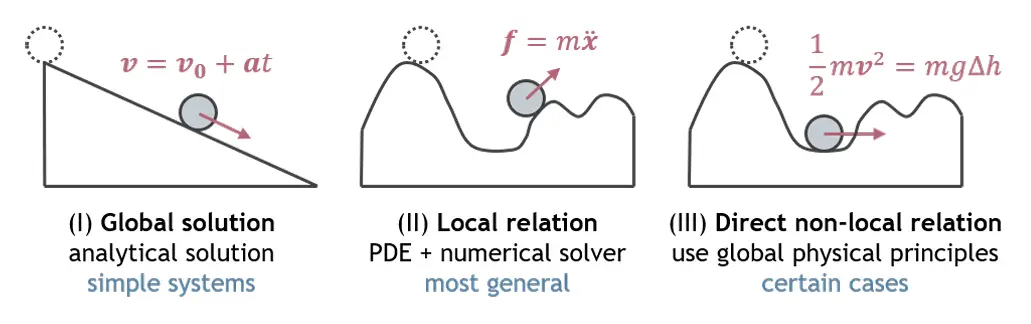
图2 .我们如何求解一个物理状态？（I）简单系统的解析解。（II）对于更复杂的物理系统，大多数物理偏微分方程只对附近时间步长的局部关系建模。（III）对于某些物理系统，即使它们在时间上不接近，状态也可以直接相关。
B. 前置工作
学习哈密顿力学 让我们从相空间坐标开始，其中是广义坐标，是广义动量或共轭动量。如果表示粒子在欧几里得坐标中的位置，那么对应于它们的线性动量。如果表示球坐标中的角位置，那么对应于相关的角动量。我们考虑时不变的哈密顿量，它是一个标量函数，满足
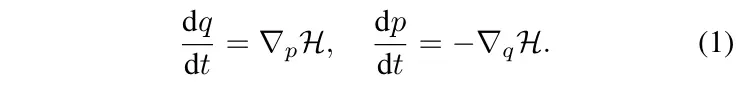
公式1被称为哈密顿运动方程，通过定义相空间中沿着矢量场的轨迹来描述系统的演化。这个场被称为辛梯度，它控制着动力学，使得沿着的运动引起哈密顿量的最快变化，而沿辛方向的运动保持系统的能量结构。
哈密顿神经网络（HNN）（Greydanus等人，2019年）将汉密尔顿函数视为由神经网络参数化的黑盒函数，并优化网络参数以最小化损失函数
从初始状态开始，可以通过对时间上的辛梯度进行积分来计算轨迹。
离散哈密顿 除了连续哈密顿量及其离散化之外，还可以直接用凸优化中的离散力学和对偶理论来定义离散哈密顿量（Gonzalez，1996）。
这里“右”意味着在时间上是向前的，在时间上是向后的。该公式用作连续哈密顿量的一阶离散近似，
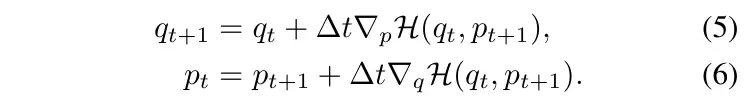
图3显示了一个离散右哈密顿网络，用于计算时间步和之间的状态关系。我们主要使用右哈密顿来描述我们的网络设计，但类似的方程可以定义左哈密顿，同样的方法也适用于。更多详情见附录A。
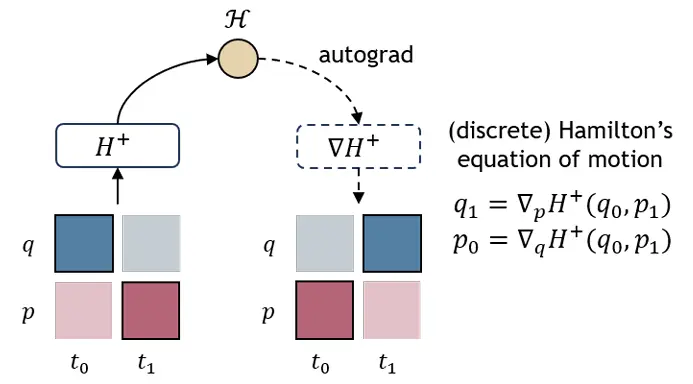
图3 .离散（右）哈密顿神经网络。深蓝色和暗红色表示网络的输入和输出。浅色表示相邻的时间步长。
以HNN为例，物理网络通常学习由更新规则建模的相邻时间步长和之间的状态关系
与正演建模相比，公式3和4中的离散化更精确，并且在时间积分下更好地保留了系统的辛结构。然而，这些更新规则的隐式性质在推理时引入了挑战，因为确定新的系统状态需要解决优化问题，当可用数据由单个模拟轨迹组成而没有附加参考点时，这变得困难。
我们的解决方案是将优化过程合并到网络中，从而得到去噪哈密顿网络（第3.4节），该网络统一了每个时间步的状态优化去噪更新规则和跨时间步的哈密顿模型状态关系。
C. 分块离散哈密顿量
我们将状态块定义为沿着时间维度级联的个状态的堆栈，其中是块大小。我们还引入步幅作为可以灵活定义的超参数，以代替等式5-6中的固定时间间隔。这种方法使网络能够捕获更广泛的时间相关性，同时保持底层的Hamilton结构。我们通过将两个重叠的系统状态块关联起来来定义我们的块离散（右）Hamilton，每个块的大小为，移位步长为
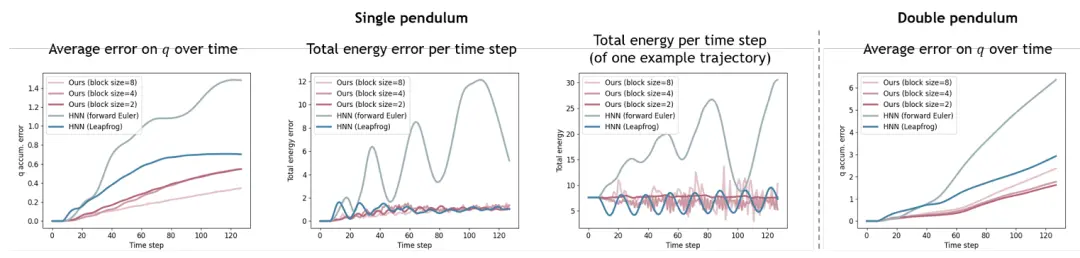
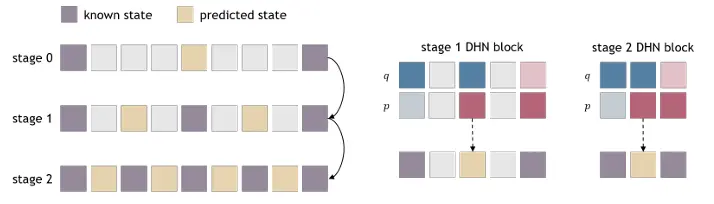
图4示出了块大小和步长的逐块离散哈密顿量。经典HNN可以被视为块大小和步长的特殊情况。，的分块哈密顿量的物理解释可以在附录B中找到。 类似于HNN，可以根据公式8-9的运动损失方程来训练逐块离散哈密顿网络
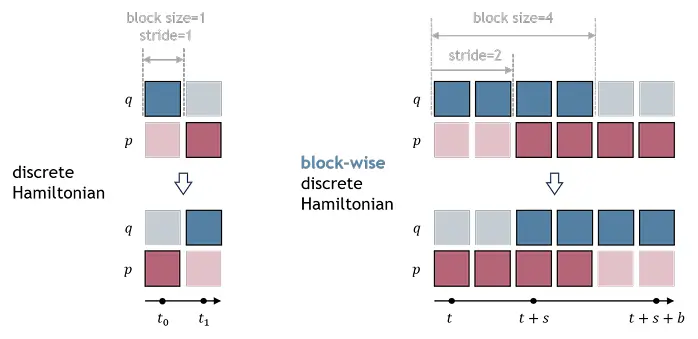
图4 .分块哈密顿算子。左：经典HNN被视为块大小和步长的特殊情况。右：离散（右）哈密顿块，，。深蓝色和暗红色表示网络输入和输出。浅色表示相邻的时间步长。
图5.去噪哈密顿块。左：输入状态的随机掩蔽。右：输入状态的随机噪声采样。不同的状态具有不同的采样噪声尺度。
D. 去噪哈密顿网络
根据我们在第3.2节中介绍的动机，我们希望Hamilton块不仅能够对跨时间步的状态关系进行建模，而且还能够学习每个时间步的状态优化以进行推理。为了实现这一点，我们采用了一种屏蔽建模策略（He等，2022），通过屏蔽一部分输入状态来训练网络（图5）。
我们不是简单地屏蔽输入状态，而是用不同幅度的噪声采样来干扰它们（图5）。这种策略确保模型学习迭代地改进预测，使其能够从损坏或不完整的观察中恢复物理上有意义的状态。具体地说，我们定义了一个噪声级递增序列。以阻塞输入状态为例，随机采样高斯噪声和每状态噪声尺度。设是二进制掩码，0表示未知状态，1表示已知状态，我们通过下式获得噪声输入
直觉上，它强制已知状态具有0的噪声尺度。在我们的实验中，去噪步骤的数量被设置为10。在推理时，我们用一系列在所有未知状态上同步的逐渐减小的噪声尺度来逐步去噪未知状态。我们应用和来迭代更新和。更多详情见附录C。
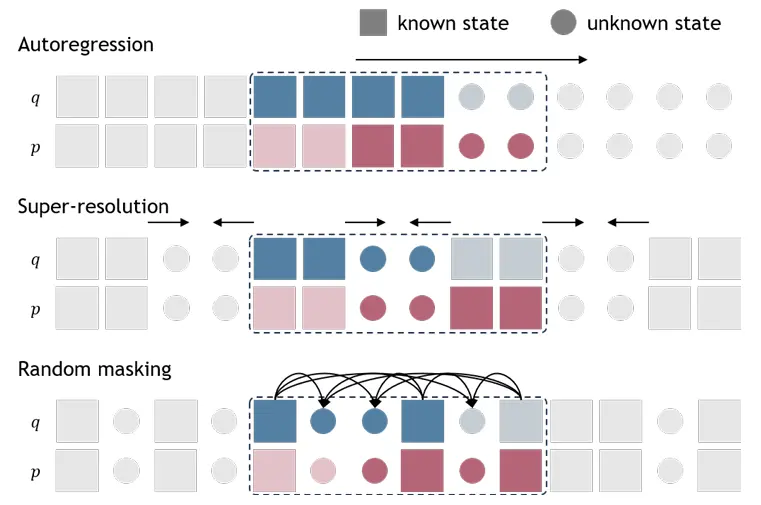
图6. 不同的掩蔽模式。使用不同的掩蔽模式进行训练可以实现不同的推理策略。虚线包围的彩色块是沿着序列沿着滑动的去噪哈密顿块。
不同的掩蔽模式 通过在训练过程中设计不同的掩蔽模式，我们可以为不同的任务定制灵活的推理策略。图6显示了三种不同的掩蔽模式：通过掩蔽块的最后几个状态的自回归，这类似于物理模拟，可以通过前向建模进行下一个状态预测;通过屏蔽掉块中间的状态来实现超分辨率，这可以应用于数据插值;以及更一般地，包括随机屏蔽的任意阶屏蔽，其中根据任务要求自适应地设计屏蔽图案。
E. 网络架构
解码器专用Transformer 对于每个哈密顿块，网络输入是不同时间步长的的堆栈，的堆栈，并且我们还为整个轨迹引入全局潜码作为条件Transformer（拉德福等人，2019; Jin等人，2024年），它类似于一个类似GPT的解码器，但没有因果注意掩模，如图7所示。我们对所有输入标记作为长度为的序列。全局潜在码用作用于输出哈密顿值的查询令牌。在我们的实验中，我们实现了一个简单的两层Transformer，它适合单个GPU。
自动解码器框架 我们采用自动解码器框架（Park等，2019），而不是依赖编码器网络从轨迹数据中推断全局潜在代码，为每个轨迹维护可学习的潜在代码（图8）。这种方法允许模型有效地存储和细化系统特定的嵌入，而不需要单独的编码过程。在训练过程中，我们联合优化网络权重和码本。训练结束后，给定一个新的轨迹，我们冻结网络权重，只优化新轨迹的潜在代码。
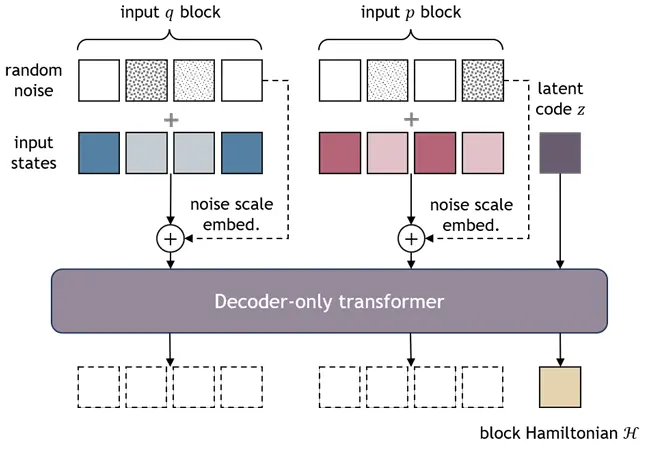
图7. 仅解码器Transformer架构。我们为每个轨迹使用一个潜在代码作为哈密顿值输出的查询令牌。每个状态的噪声尺度被编码并添加到位置嵌入中。深紫色（所有阴影）表示可训练的模块或变量。
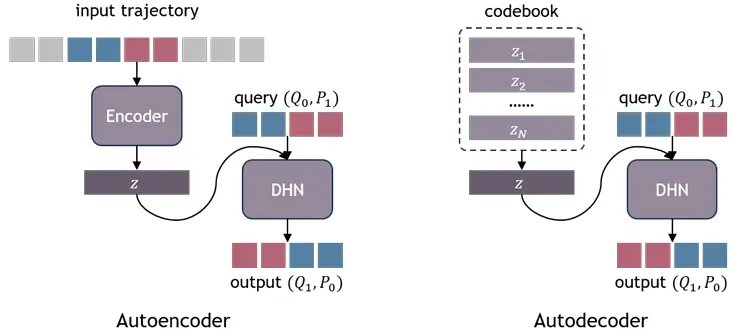
图8.自动解码器。我们没有使用编码器对输入轨迹进行编码，而是为整个数据集维护一个码本，每个轨迹都有一个可学习的潜在代码。深紫色（所有阴影）表示可训练的模块或变量。
Ⅳ 实验
我们用单摆和双摆两种设置来评估我们的模型。这两种设置都包括模拟轨迹的数据集。单摆是一个周期系统，每个状态的总能量可以直接从计算，因此我们用它来评估模型的能量守恒能力。双摆是一个混沌系统，小的扰动可以导致未来状态的发散。
与以前的作品不同（Toth等人，2019年），其使用固定的系统参数集生成数据，同时改变初始条件，我们在保持初始状态不变的情况下，通过改变弦的长度来引入变分（附录图18）。这种修改评估了模型是否可以推广到更广泛的参数化动态系统，而不是拟合到单个参数化动态系统。实例系统。对于这两种设置，我们将数据集分为1000个训练轨迹和200个测试轨迹。每个轨迹被离散化为128个时间步。更多细节可以在附录D中找到。
我们用对应于图6中的三种不同掩蔽模式的三种不同任务来测试我们的模型。（自回归）的正向模拟，（ii）表示学习与随机掩蔽的物理参数推断，和（iii）渐进超分辨率的轨迹插值。这些任务突出了DHN的适应性，以各种物理推理的挑战，测试其能力，产生，推断，并在不同的观测约束条件下插入系统动态。
A. 正演模拟
我们从正向模拟任务开始，在给定的初始条件下，模型逐步预测物理系统的未来状态。我们通过在每个DHN块中应用掩蔽策略来实现这一点，其中最后几个令牌在训练期间被掩蔽，需要模型迭代地细化和去噪它们（图6顶部）。对于块大小为B且步幅为s的一个DHN块，掩码被应用于最后个令牌。在推断时，给定时间步长处的已知状态，我们将DHN块应用于时间步长，其中我们使用已知状态来预测未知状态。我们用块大小，步长。
拟合已知轨迹 我们首先用前向建模来评估模型表示已知物理轨迹的能力。在这个实验中，我们训练模型来拟合1000个训练轨迹，我们通过给出每个轨迹的前8个时间步并使用模型预测未来120步来进行测试。由于所有模型都只使用附近时间步的状态进行训练，（基线的相邻时间步长对，DHN的状态块），小的拟合误差可以在正演建模中随着时间积累。除了网络固有的累积预测误差之外，数值积分近似也会引起不准确性，这会随着时间放大偏差。
图9显示了我们的模型在不同块大小下的结果，与HNN相比（Toth等，2019）。左和右是单摆和双摆系统在每个时间步的预测的均方误差（MSE），中间的图显示了一个示例轨迹上的平均总能量误差和总能量的演变。虽然HNN是辛的，在保证能量守恒的网络中，数值积分器仍然会引起不可控的能量漂移。这种额外的数值误差在前向方法中是特别不可避免的。虽然这可以通过隐式状态优化的变分积分方法来解决，但优化的收敛依赖于所有可能状态的知识，包括不在轨迹上的状态，这大大增加了训练网络的数据消耗。对于我们的DHN，每个时间步的状态优化由去噪机制建模，而不需要变分积分器。当块大小为2时，模型的总能量保持稳定，增大块大小会引起较长时间范围内的能量涨落，但这种涨落并没有表现出明显的能量漂移倾向。
图9. 正演模拟：拟合已知轨迹。我们的方法的结果以粉红色显示，具有不同数值积分器的HNN的结果以不同的蓝色阴影显示。第1列：单摆的平均状态预测误差。第2列：单摆系统的总能量可以很容易地用每个时间步长的状态解析计算。我们比较了每个时间步的网络预测状态和地面真实状态的总能量。第3列：一个示例轨迹上随时间步的预测总能量。第4列：双摆的平均状态预测误差。
在新轨迹上完成 接着我们在具有部分观察值的新轨迹上评估我们的模型。具体地说，我们给出每个测试轨迹中的前16个时间步，并使用它们来优化每个轨迹的全局潜码，并冻结网络权重，如第3.5节所述。优化这些潜码后，我们使用它们来预测接下来的112个时间步。这个任务评估DHN从稀疏的初始观测推断系统动态和准确预测未来状态的能力。
图10显示了我们与HNN（顶行）和各种没有物理约束的基线模型（底行）的比较结果。与两个基线相比，我们的小块DHN显示了更准确的状态预测和更好的能量守恒。大块大小可能会导致长时间范围内的错误爆炸，因为我们简单的2层网络很难适应非常复杂的多状态关系。
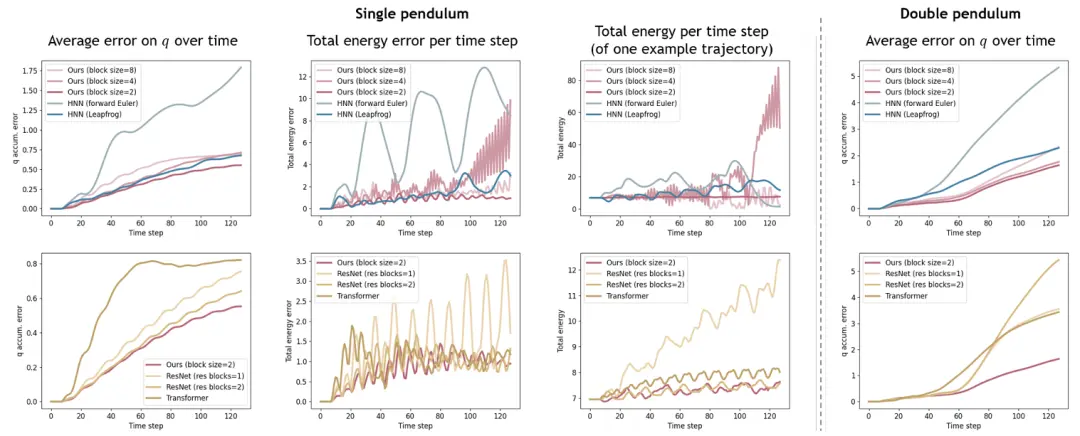
图10. 正演模拟：完成新的轨迹。顶行：比较我们的方法（粉红色）和具有不同数值积分器的HNN（以蓝色显示）。我们的方法之间的比较（以粉色显示）和具有不同架构的普通网络（黄色显示）。香草网络直接预测下一个状态。注意，两行之间的轴比例是不同的。
B. 表示学习
接下来，我们测试模型有效编码和区分不同物理系统参数的能力。去噪和随机掩蔽是自监督学习中成熟的技术，在语言建模（Devlin，2018）和视觉（Vincent等，2008; He等，2022）中产生最先进的表示。在这里，我们应用随机掩蔽模式（图6底部）并研究类似的范例是否可以增强动态物理系统中的表示学习。
为了量化学习到的表示的质量，我们遵循计算机视觉中广泛采用的自监督表示学习范式（Chen等人，2020; Oord等人，2018; He等人，2020; Kolesnikov et al，2019）进行特征预训练和线性探测。具体来说，我们使用训练集在码本旁边预训练自动解码器，然后冻结学习的表示，并在上面训练一个简单的线性回归层来预测系统参数。这种方法评估DHN的潜在代码是否捕获有意义的物理属性。我们在双摆系统中进行实验，并预测长度比（附录图18）。由于该物理量具有无量纲特性，在数据预处理的尺度归一化过程中能保持不变。
图11显示了我们的DHN在不同块大小下的线性探测结果（）。与基线网络相比，我们的模型实现了更低的MSE。如图4所示，HNN可以被视为我们的哈密顿块的特殊情况，其内核大小和步长为1，在这个双摆系统中，块大小为4是推断其参数的最佳时间尺度，而块大小为4的时间尺度是系统参数的最佳时间尺度。
图12示出了具有不同块大小和步长的DHN的结果。如在12b中，哈密尔顿块的输入和输出状态具有时间步长的重叠区域。哈密尔顿块的广义能量守恒依赖于具有相同输入和输出的重叠区域。在训练期间，这种约束作为状态预测损失的一部分施加在网络上。较大的重叠对网络施加了更强的正则化，但鼓励网络实施更多的这种自相干约束，而不是更多的状态间约束。相反，减少重叠同时增加步幅鼓励模型合并来自时间上更远的状态的信息，但代价是较弱的自相干约束，这可能影响稳定性。在重叠等于块大小且步幅为零的极端情况下，DHN块具有相同的输入和输出，训练损失退化为自相干约束。HNN是另一种零的特殊情况重叠（因为块大小为1，重叠只能为零）。如图12b所示，对于我们的简单双层Transformer，最佳块大小和步长约为，并具有适度的重叠量。
图11. 潜在代码的线性探测（MSE↓）。我们通过对全局潜在代码应用线性回归层来预测。
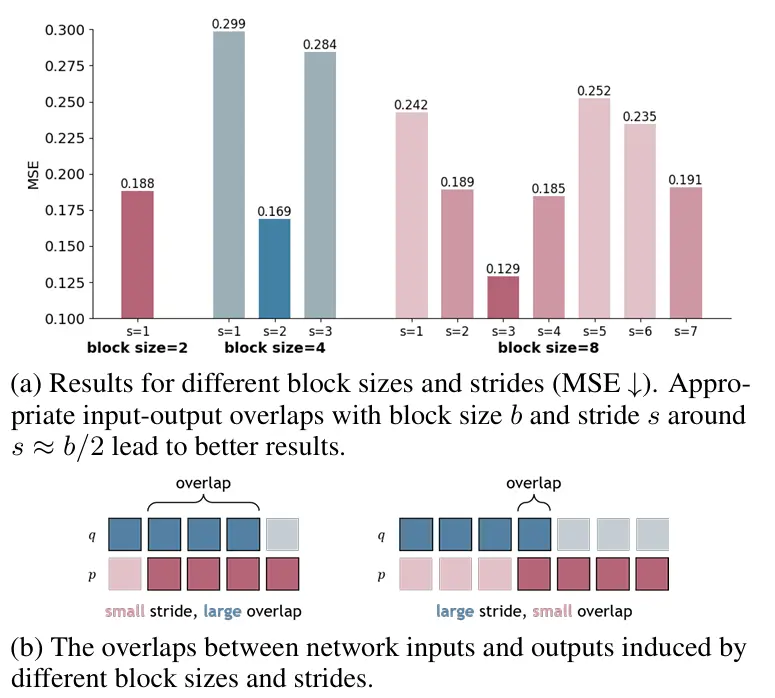图12. 不同DHN参数的线性探测。(a)不同块大小和步长（MSE↓）的结果。块大小
和步长在附近的适当输入输出重叠会导致更好的结果。(b)由不同的块大小和步长引起的网络输入和输出之间的重叠。
图13. 插值为渐进式超分辨率。左：2×超分辨率的三个阶段重复两次。右：不同稀疏度的不同阶段的DHN块。
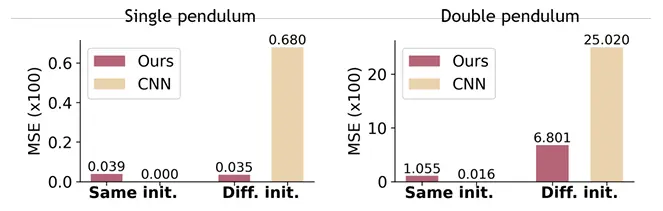
图14. 插值（超分辨率）结果（MSE↓）。我们将DHN（Ours）的性能与基于CNN的实现（CNN）进行了比较。所有MSE值均按100缩放，以提高图中十进制表示的精度。
C. 轨迹插值
为了证明DHN块的灵活性，我们展示了轨迹插值（超分辨率）。我们通过重复应用2×超分辨率来进行4×超分辨率。如图13左图所示。我们构建了一个的DHN块。不同稀疏度的轨迹块如图13右侧所示。掩模应用于中间状态，并且侧边的两个状态已知。
每个轨迹都与所有三个超分辨率阶段的共享全局潜码相关联，从而形成训练集的结构化码本。在训练期间，网络权重和这些潜码都在渐进细化阶段(0,1,2)中联合优化。在推理时，给定仅在稀疏层（阶段0）具有已知状态的新轨迹，我们冻结DHN块中的所有网络权重，并使用阶段0对全局潜在代码进行优化。在此测试时间优化（自动解码）之后，我们应用阶段1、2 DHN块来逐步对已知状态之间的未知状态进行降噪。
我们使用两种测试设置来评估模型：（i）与训练轨迹具有相同初始状态的轨迹，以及（ii）未知初始状态的轨迹。为了设置这一点，我们将所有训练轨迹裁剪到时间步长。对于测试集中的每个轨迹，我们将其分为两段：时间步长和，前者具有与训练集相同的初始状态，而后者具有不同的初始状态。
我们将我们的模型与卷积神经网络（CNN）进行了超分辨率比较。图14显示了我们的结果。对于与训练数据具有相同初始状态的轨迹，两种模型都显示出较低MSE的良好插值结果。基线CNN显示出稍好的结果，因为它本身没有正则化，并且可以很容易地过拟合训练轨迹。对于具有未知初始状态的测试轨迹，CNN很难泛化，因为它的插值严重依赖于训练分布。相比之下，DHN表现出很强的泛化能力，因为它的物理约束表示使它能够推断出合理的中间状态，即使在分布变化。
Ⅴ 讨论与结论
平衡灵活性与物理约束对于推进基于物理的学习至关重要。正如NLP和视觉中的统一架构（例如，transformers）在保持核心归纳偏差的同时适应不同的任务，我们探索单个模型是否可以处理从全局参数推断到局部状态关系的任务，而不牺牲物理一致性。
我们研究的一个关键问题是：深度学习中的物理推理是什么定义的？除了下一个状态预测，它还包括参数估计，系统识别和发现动态系统中的高层关系。我们设想基于物理的学习朝着适应性强的框架发展，在保持物理严谨性的同时，在任务之间流畅地过渡。
我们重新考虑的另一个核心概念是：什么是物理模拟？模拟传统上被视为一个顺序过程，其中轨迹从初始状态逐步展开。我们将其重新表述为全局，时间一致的重建，从最近的视频生成模型中汲取灵感，这些模型对完整序列进行降噪，而不是逐帧预测（Chi et al，2023）。
我们还研究了：神经网络应该具备哪些物理属性？虽然基于偏微分方程的方法会施加局部约束，但我们的研究结果表明，关键的物理属性可以通过数据驱动的学习出现，就像视觉模型在没有明确对象检测器的情况下推断语义一样。
虽然我们目前的工作为基于哈密顿的网络设计提供了更大的灵活性，但我们也认识到了某些局限性。一个关键的局限性是计算成本：我们的模型需要比基线变压器更密集的梯度计算。此外，目前的实验集中在具有简单时间动态的小尺度系统上。缩放到复杂的空间-时间系统可以受益于由现代视觉模型启发的分层或基于注意力的体系结构。
我们相信，基于物理的学习正处于一个重大变革的边缘，类似于视觉和自然语言处理中自我监督学习的兴起。通过将物理推理重新定义为一个重构问题-从部分或损坏的输入中预测系统状态-我们朝着一个统一的建模范式迈进，将深度学习的灵活性与物理定律的严谨性融合在一起。
影响声明
这项工作旨在通过开发基于物理推理的人工智能工具来推进科学研究。通过将物理约束纳入神经网络，我们寻求提高基于学习的模型的科学应用的可解释性和可靠性。然而，与其他机器学习方法一样，将神经网络应用于科学问题需要谨慎。神经网络可能会表现出幻觉或虚假相关性，如果没有得到适当的验证，可能会导致误导性的科学结论。
虽然强制执行物理约束可以增强对AI驱动建模的信任，但它并不能消除对严格验证的需求，特别是在分析实验数据时。用户必须注意学习表示的局限性，并确保从AI辅助分析中得出的结论得到物理原理和经验验证的支持。
致谢
我们感谢Rell the cat为图1提供的照片，同时感谢尹天为、张天源、Shivam Duggal、李一辰、Carolina Cuesta-Lazaro和Katherine L. Bouman富有建设性的讨论。邓成和L. Guibas的部分研究工作得到丰田研究院University 2.0计划及范内瓦·布什教席学者基金的资助；冯柏尧和W. T. Freeman的科研工作部分受NSF Award 2019786（NSF人工智能与基础交互研究所）及NSF CIF Award 1955864（计算成像中的遮挡与方向分辨率）支持；C. Garraffo的研究由哈佛-史密松天体物理中心AstroAI项目资助；A. Garbarz的科研工作受阿根廷国家科学与技术研究委员会(CONICET)及布宜诺斯艾利斯大学(UBA)支持，资助编号包括PICT 2021-00644、PIP 11220210100685CO和UBACYT 20020220400140BA；R. Walters的研究得到NSF 2134178项目资助。
参考文献
来源：同济智能汽车研究所
