近几年,对传统载货汽车车架的设计、分析及优化越来越受重视,与产品开发的联系也越来越紧密,但针对新能源载货汽车尤其是增程式新能源车型货车车架分析还未见报道。本文作者首先对某新能源载货车车架进行模态试验,接着建立了有限元分析模型对结果有效性进行验证,然后进行车架刚、强度分析,结果表明车架结构满足设计要求,最后对原有车架模型进行灵敏度分析,车架轻量化效果明显。
1 新能源载货车车架
新能源载货车车架与传统货车车架作用类同,既要承受来自路面的各种冲击载荷,又要承载各种质量的部件。文中研究对象与传统燃油车不同的是该增程式新能源货车车架不仅包含发动机、底盘、车身等传统件,而且也囊括了动力电池、电机及电控等新能源部件,增加了车架承载的复杂性。
2 车架实车试验
模态分析用来确定车架的振动特性(频率和振型)。车架自身可以看成一个多自由度的弹性振动系统,对其进行模态分析的目的就是为了避免共振。
文中通过试验来获得某新能源载货车车架的模态。此次模态试验采用的设备如表1所示。
表1 试验设备

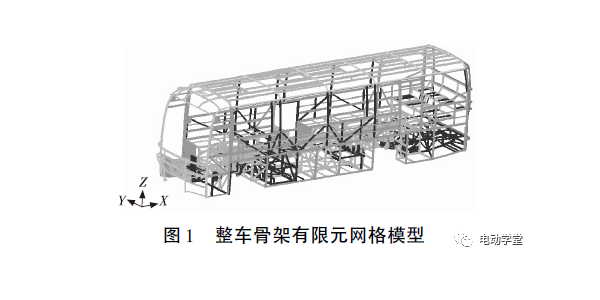
试验车架是在整车约束状态下,分别在车架纵梁和横梁上表面位置处布置相应的三向加速度传感器,共计29个测点(见图1),其试验几何模型如图2所示。选择车架左前23测点和右后11(见图3)测点附近分别进行X、Y、Z向锤击,每个方向进行7次激励,对测试信号求平均,得出相应点与测试点间的频率响应函数。采样带宽设置为64 Hz,频率分辨率设置为0.25 Hz,输入加力指数窗,输出在采样周期内充分衰减,加矩形窗即可,H1估计方法。试验测试结果如图4—图6所示。

图1 车架模态测点
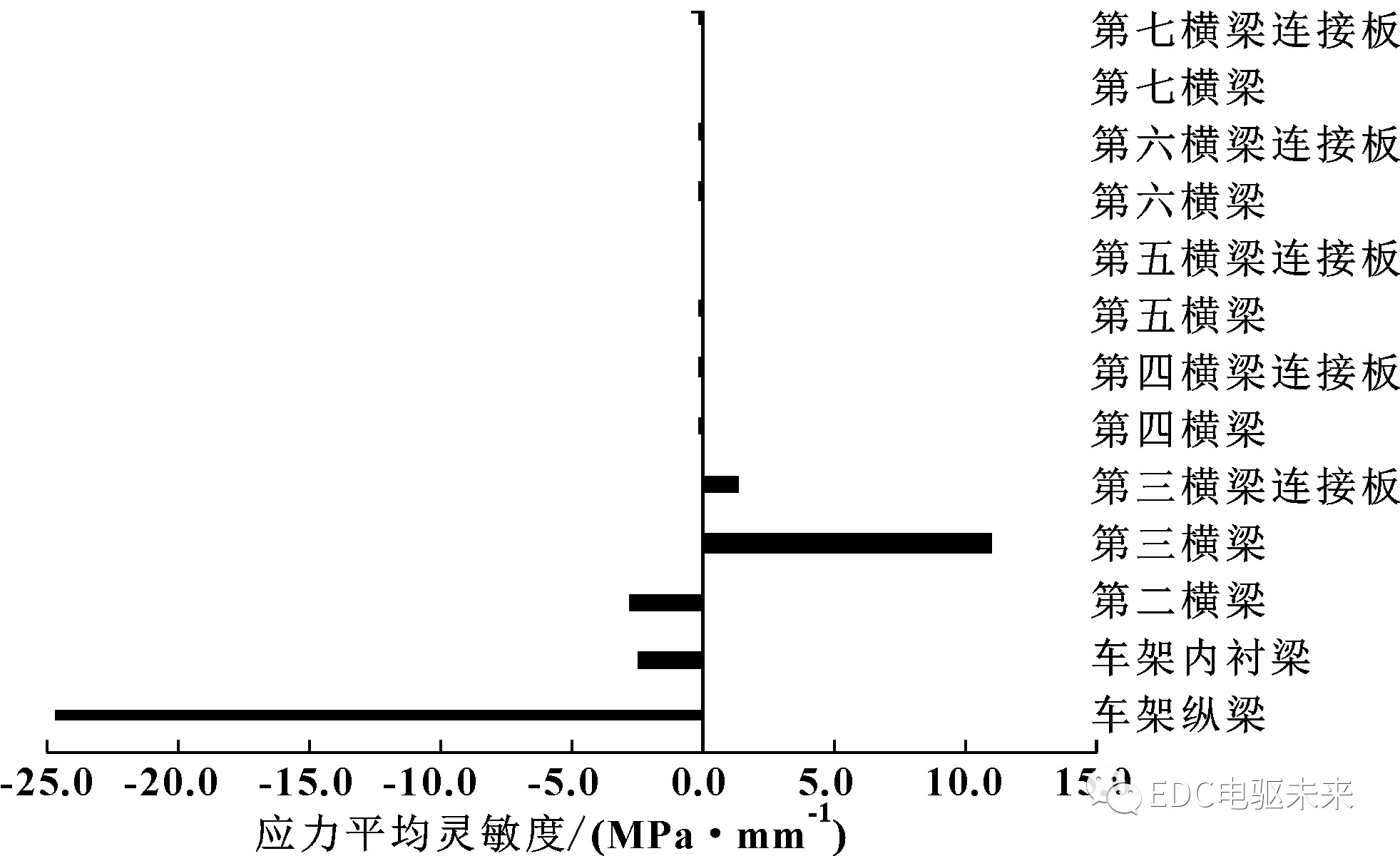
图2 试验几何模型

图3 锤击点

图4 车架一阶扭转
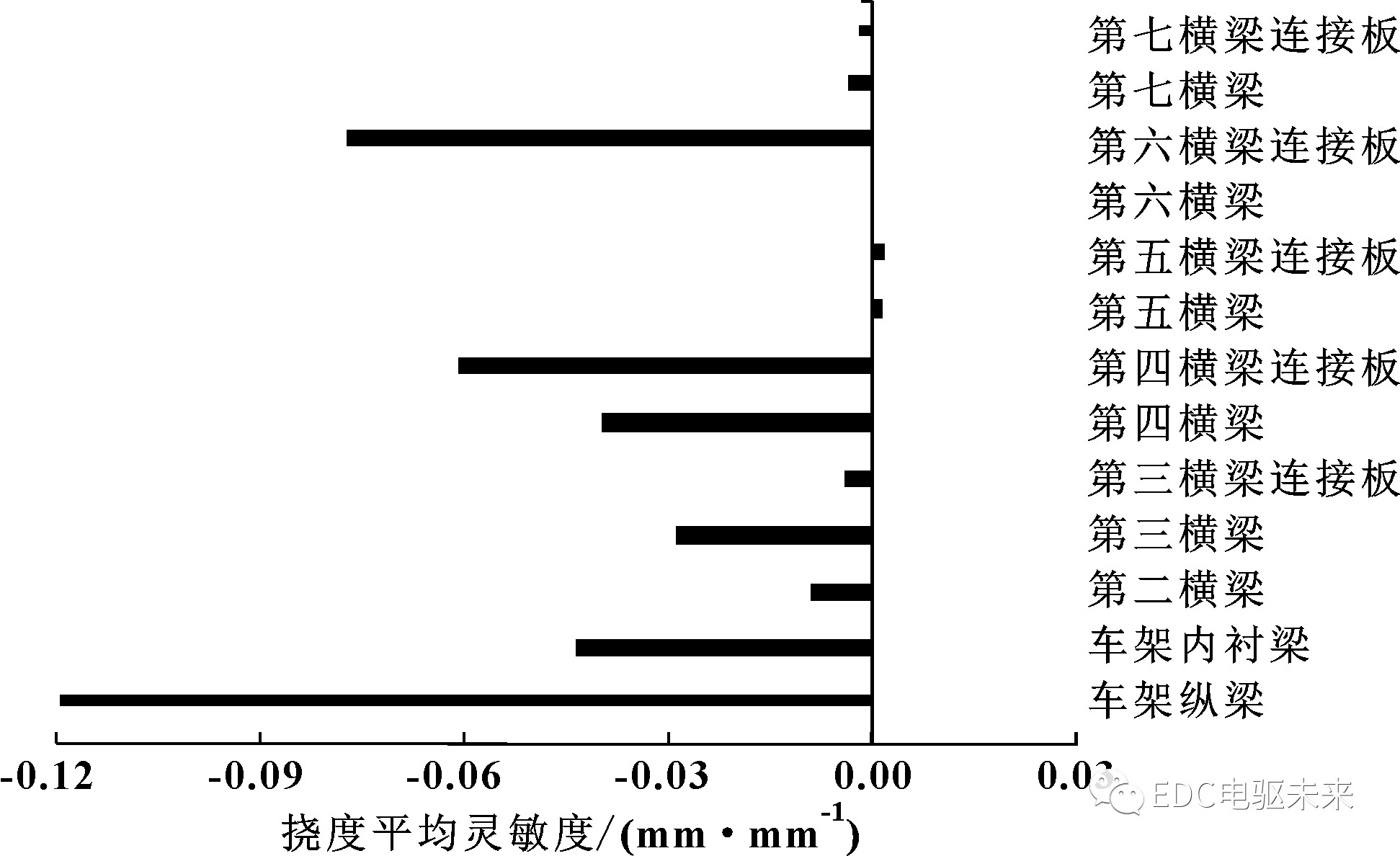
图5 车架Y向一阶弯曲

图6 车架Z向一阶弯曲
由试验结果可知,该车架的一阶扭转模态频率为8.66 Hz,一阶侧向弯曲模态频率为17.89 Hz,一阶垂向弯曲模态频率为25.20 Hz。
3 车架仿真分析
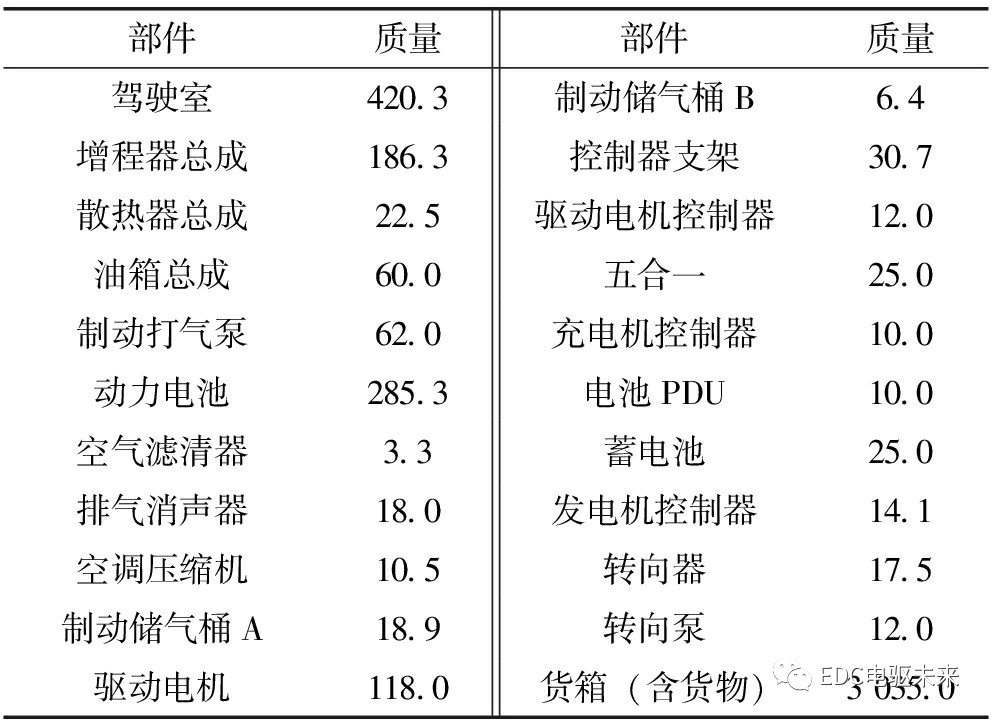
根据模态试验情况,对上述增程式新能源载货车车架进行有限元仿真建模分析。在创建有限元模型时,根据需要对某些几何细节进行简化处理,如对小倒角(<R5 mm)、小孔(<φ6 mm)或非关键部位的细节特征进行忽略,根据经验对某些初步判断不影响或者对计算结果影响可以忽略的细微特征进行简化。对几何模型进行合理离散化满足标准:螺栓、焊接等连接采用刚性RBE2单元模拟;桥、板簧主体部分采用梁单元(CBEAM)模拟,吊耳与板簧之间采用弹簧单元(CELAS1)模拟;各相关零部件的质量通过在其质心位置加载质量单元(CONM2)与车架通过RBE3固连来实现。有限元模型的材料参数及部件质量信息分别如表2、表3所示。
表2 材料参数

表3 某新能源载货车部件质量信息 kg
3.1 车架模态分析
车架模态试验在整车装配状态下进行,文中有限元仿真模型(见图7)通过约束轮心位置自由度来计算车架总成的约束模态。在车架结构动态分析中,由于低频振动比高频振动特性对车架结构影响大,因此文中采用Block Lanczos法提取车架总成前10阶模态(限于篇幅,只列出与试验相近3阶,见图8—图10)。
由仿真结果可知,车架总成的一阶扭转模态频率为7.79 Hz(与试验误差9.8%),一阶侧向弯曲模态频率为18.55 Hz(与试验误差3.5%),一阶垂向弯曲模态频率为25.95 Hz(与试验误差2.9%)。仿真与试验结果相近,证明了有限元仿真模型的准确性。

图7 有限元计算模型
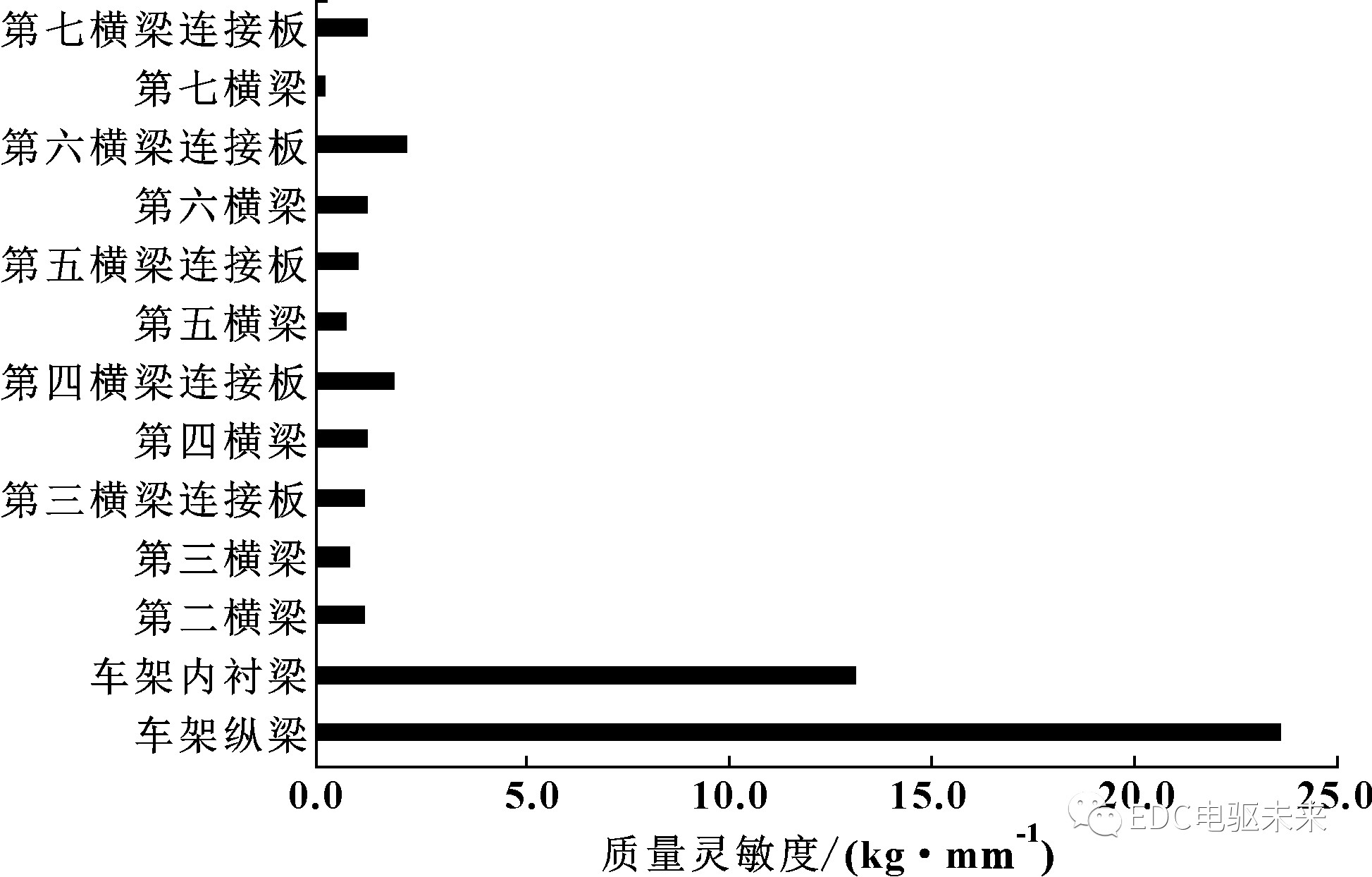
图8 一阶扭转
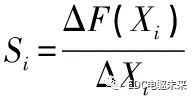
图9 一阶侧向弯曲
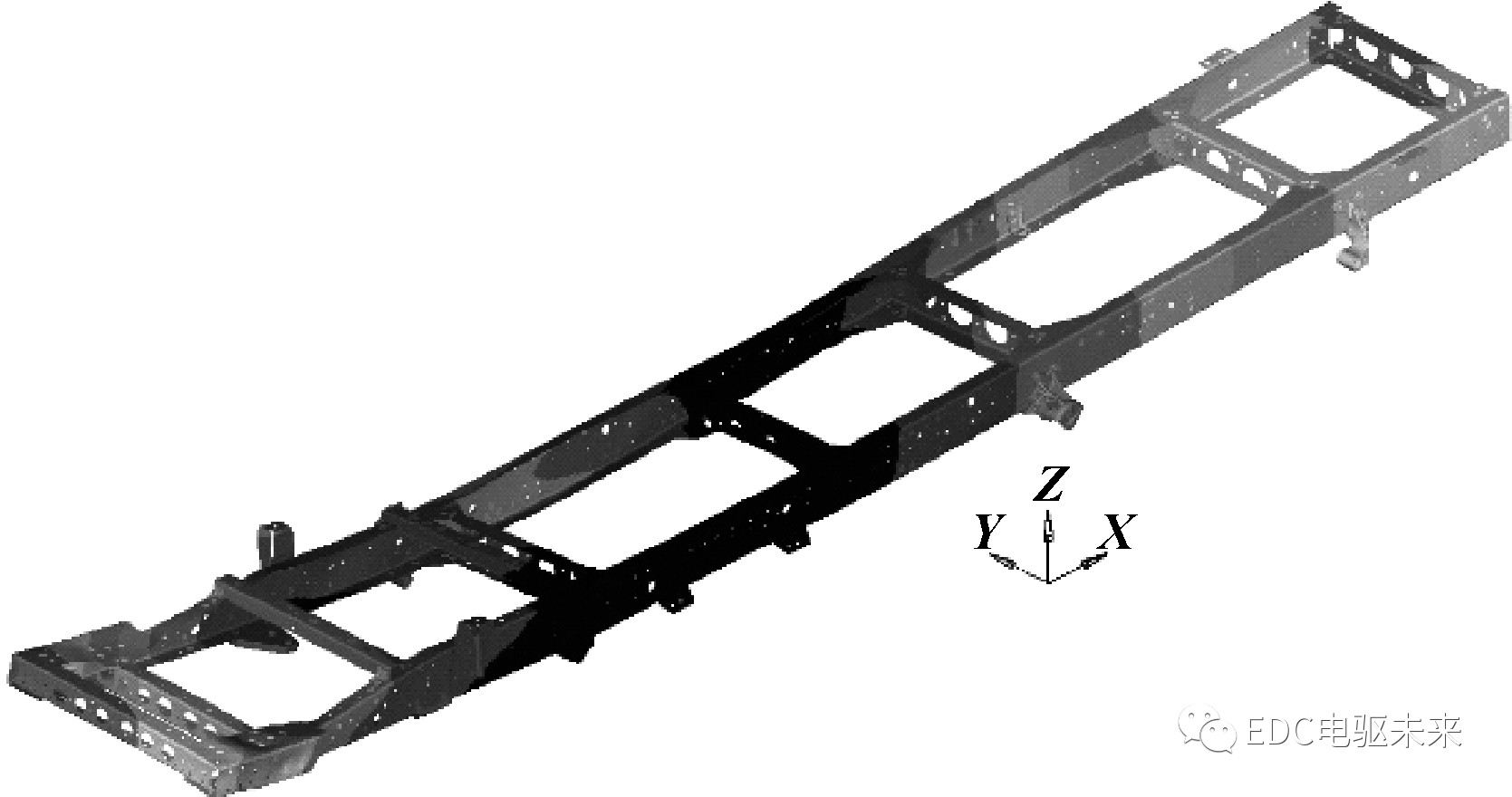
图10 一阶垂向弯曲
3.2 车架刚度校核
车架刚度是评价车架性能的一项主要指标,它对车架强度、NVH、可靠耐久性等都有着至关重要的影响。车架总成在各种载荷工况下,最常见情况为弯曲及扭转变形,所以在车架设计时,选取其弯曲刚度、扭转刚度(模量)作为衡量车架性能的考察指标。本文作者根据表4刚度分析工况创建弯曲刚度、扭转刚度有限元计算模型,分别如图11、图12所示。
表4 刚度分析工况定义


图11 弯曲刚度计算模型
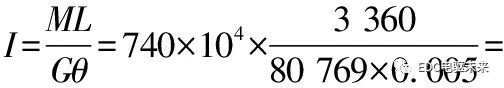
图12 扭转刚度计算模型
弯曲刚度计算如下:
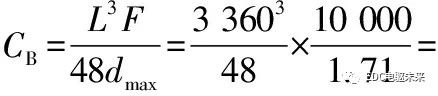
4.6×1012 N·mm2 >2×1012 N·mm2
式中:CB为弯曲刚度(N·mm2);L为前后板簧中心距(mm);F为加载力(N);dmax为加载点最大变形量(mm)。
扭转模量计算如下:
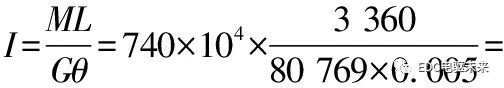
6.17×107 mm4 >3×106 mm4
式中:I为扭转模量(mm4);M为前桥施加的扭矩(N·mm);L为前后桥轴距(mm);G为车架材料剪切模量(MPa);θ为扭转角度(rad)。
综上,车架总成的弯曲刚度及扭转模量满足设计要求。
3.3 车架静强度分析
在汽车行驶过程中,承受复杂多变的载荷,对车架进行设计时,要保证其在最大载荷工况下不能被破坏或者有较大的塑性变形。文中创建了强度分析有限元模型(见图13),并选取了满载状态下的4种行驶工况进行模拟(见表5)。
通过计算分析可知:垂向冲击工况(见图14,其余工况图略)最大应力为331 MPa,侧向冲击工况最大应力为163.6 MPa,紧急制动工况最大应力为160.8 MPa,均在左前板簧前支座及左纵梁连接的第三横梁左连接板下侧;扭转工况最大应力为328 MPa,出现在前板簧后支架及右纵梁连接的第三横梁右连接板下侧,满足结构设计要求。
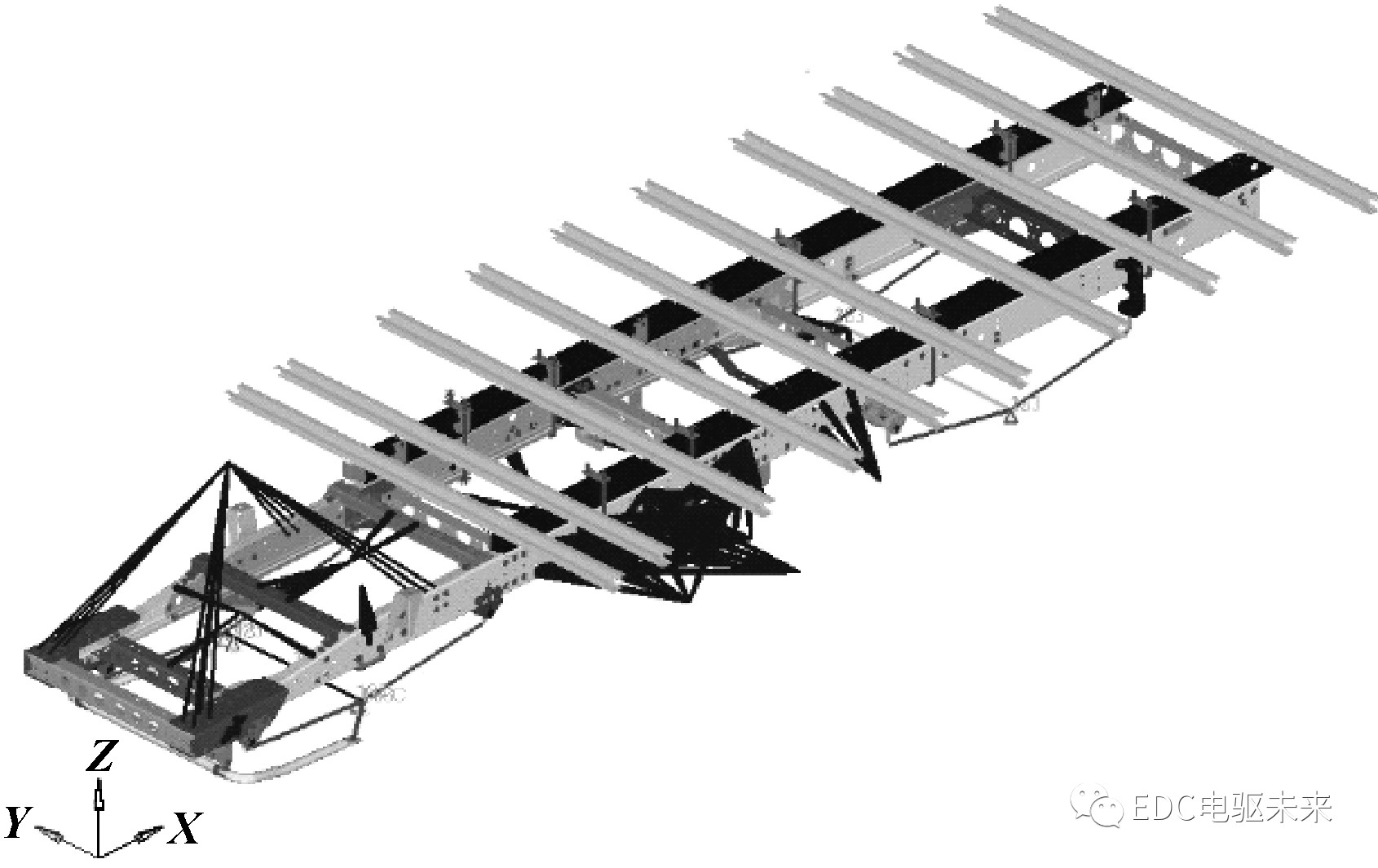
图13 强度分析有限元模型
表5 车架静强度分析工况


图14 垂向冲击
3.4 车架灵敏度分析及轻量化设计
灵敏度在数学上的意义就是针对某函数F(X)的设计变量Xi求偏导,其一阶灵敏度Si在连续状态下表示[6]为
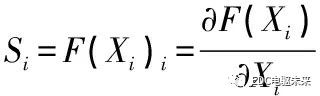
离散状态下,Si可以表示为
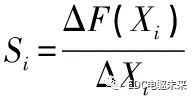
式中:i为设计变量数量,i=1,2, ......,n。
由于车架结构具有对称性,为了减少设计变量,缩短运算时间,相对应左右位置的厚度属性设置为同一个设计变量,一共有13个设计变量;车架一阶扭转频率、垂向弯曲工况变形挠度及最大应力、侧向弯曲工况变形挠度及最大应力、扭转变形工况挠度及最大应力、紧急制动工况为状态变量,总质量最小为目标函数,利用优化设计软件的最优梯度工具进行一阶差分灵敏度分析,提取各工况(求解子步)下质量、频率、挠度、应力等参数对设计变量的灵敏度。若某项设计变量的灵敏度计算结果值为正,表明随设计变量数值增大、计算结果增大的值;若为负数,则表示随设计变量数值增大、计算结果减小的值。
由表6及图15—图18可看出:车架纵梁、车架内衬梁的质量灵敏度最大,其余变量差距不大;对车架总成一阶扭转频率灵敏度影响由大至小依次为车架纵梁、第三横梁连接板、车架内衬梁、第六横梁连接板、第三横梁、第七横梁、第五横梁、第五横梁连接板、第二横梁、第四横梁、第四横梁连接板、第七横梁连接板、第六横梁;对车架挠度灵敏度影响由大到小依次为车架纵梁、第六横梁连接板、第四横梁连接板、车架内衬梁、第四横梁、第三横梁、第二横梁、第三横梁连接板、第七横梁、第五横梁连接板、第七横梁连接板、第五横梁、第六横梁;应力灵敏度影响排名前五由大到小依次为车架纵梁、第三横梁、第二横梁、车架内衬梁、第三横梁连接板。
优化后静强度分析结果:垂向冲击工况最大应力为305.4 MPa,在第二横梁及左前板簧前支座连接的左纵梁下翼面上;侧向冲击工况最大应力为279.3 MPa,在第五横梁右连接板腹面靠上侧;扭转工况最大应力为322.6 MPa,出现在前板簧后支架及右纵梁连接的第三横梁右连接板下侧;紧急制动工况最大应力为135.4 MPa,在左前板簧前支座及左纵梁连接的第三横梁左连接板下侧,均满足设计要求。
优化后,车架弯曲刚度为3.99×1012 N·mm2,扭转模量为1.24×107 mm4,两者都小于优化前,但均满足设计要求;车架总成优化前质量为289 kg,优化后质量为262 kg(质量减小27 kg),降重9.3%。
表6 灵敏度数值
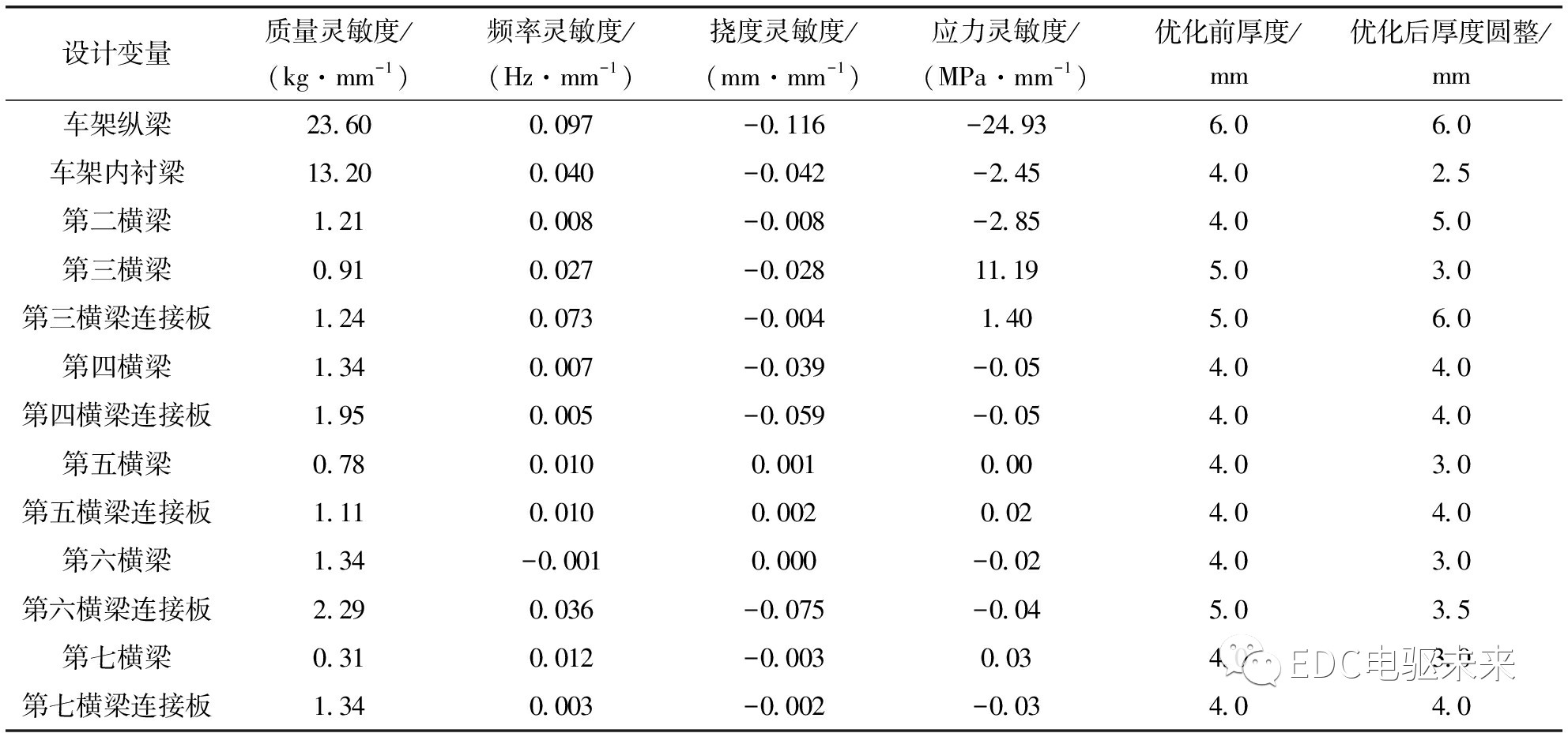

图15 质量灵敏度
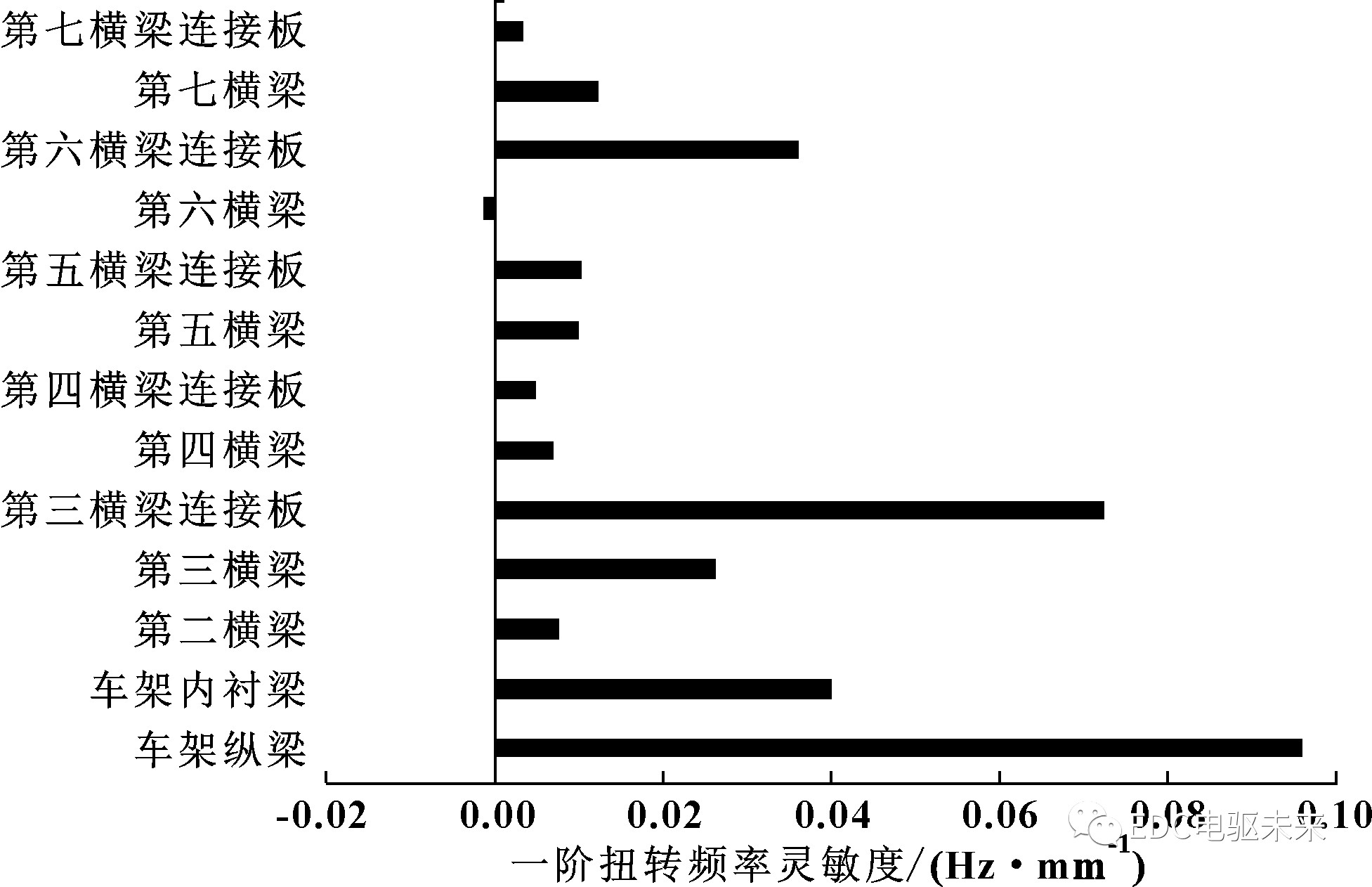
图16 一阶扭转频率灵敏度

图17 挠度平均灵敏度

图18 应力平均灵敏度
4 结论
对某新能源载货车车架性能进行了分析:
(1)通过模态试验得出某新能源载货货车车架受关注的模态振型及频率,经过有限元模型计算验证,结果符合度良好。
(2)分析了原有车架总成结构的刚度、强度,结果表明均满足设计要求。
(3)在原有车架总成基础上进行灵敏度分析,以达到轻量化目的,在满足设计要求的前提下,车架总成减重27 kg(降重9.3%),效果明显,可为工程实践提供参考,后续考虑计算该车架疲劳性能。
来源:EDC电驱未来
作者:吴成平