模 态 假 设
模态假设包括:线性假设、时不变性假设、互易性假设、可观测性假设。
线性假设:
结构的动态特性是线性的,就是说任何输入组合引起的输出等于各自输出的组合,其动力学特性可以用一组线性二阶微分方程来描述。
时不变性假设:
结构的动态特性不随时间变化,因而微分方程的系数是与时间无关的常数。
可观测性假设:
这意味着用以确定我们所关心的系统动态特性所需要的全部数据都是可以测量的。
互易性假设:
结构应该遵从Maxwell互易性原理,即在q点输入所引起的p点响应,等于在p点的相同输入所引起的q点响应。
2 、EMA、OMA、ODS
试验模态分析(Experimental Modal Analysis, EMA)
l 力锤激励EMA技术
l 激振器激励EMA技术
工作模态分析(Operational Modal Analysis, OMA)
工作变形模态(Operational Deflection Shape, ODS)
3、SISO、SIMO、MIMO
SISO:设置1个响应测点,力锤激励遍历所有测点,也称为SRIT。
SIMO:设置若干响应测点,力锤激励遍历所有测点,也称为MRIT;用一个激振器固定在某测点处激励结构,测量所有测量自由度的响应,经FFT快速测量计算FRF。
MIMO:用多个激振器激励结构,测量所有测量自由度的响应,经FFT快速测量计算MIMO-FRFs,输入能量均匀,数据一致性好,能分离密集和重根模态,在大型复杂或轴对称结构模态试验尤为重要。
模 态 分 析 基 本 步 骤
建立模型:确定测量自由度、生成几何、确定各类参数:BW,参考点、触发等。
测量:FRF,(时域数据可选)。
参数估计:曲线拟合、参数提取。
验证:MAC、MOV、MP等。
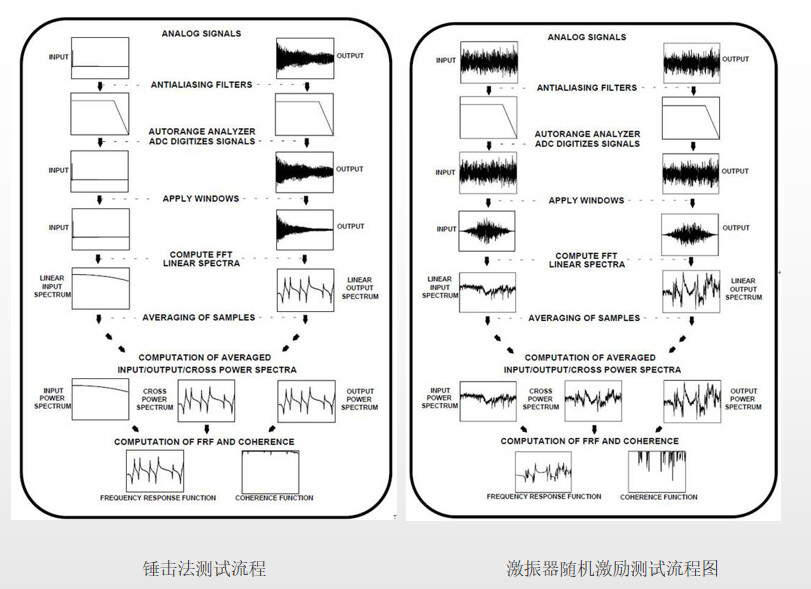
无论是锤击法测试还是激振器测试,都需将捕捉到的时域数据通过FFT变换转换到频域。FFT变换为输入和输出信号提供线性傅立叶谱(注意这些函数都是复值函数)。这将提供输入自谱(Gxx),输出自谱(Gyy)和输入-输出的互谱(Gyx)。这三个谱使用各自的时域数据进行平均。一旦得到Gxx、Gyx和Gyy,那么就可计算频响函数和相干了。
测 点 布 置 原 则
总原则:需要测量足够数目的测点,使得能唯一地描述所有你想获得的系统模态振型
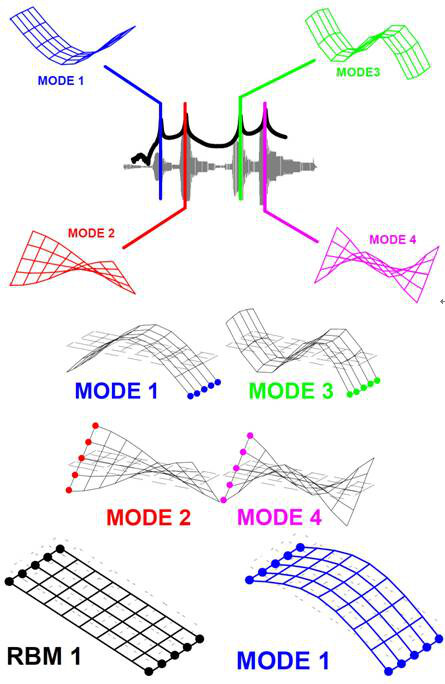
空 间 混 叠
空间上布置的测点数目过少,造成多阶(>=2)模态振型相同,不能唯一区别关心的各阶模态振型
几 何 模 型 的 作 用
表征测点的位置,非结构模型,线框模型,非实体模型,用于表征振型动画
节 点
节点位置是响应为零的位置
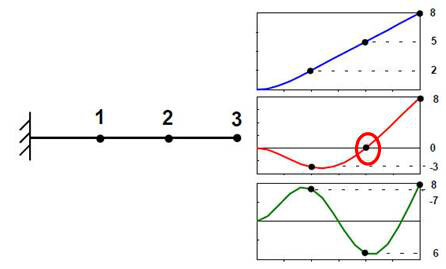
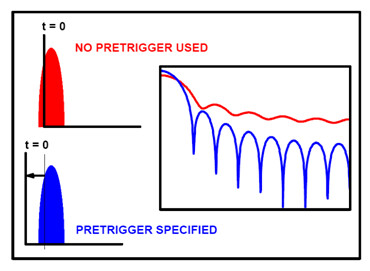
触 发、预 触 发
力 锤 法 和 激 振 器 法 的 不 同 之 处
力锤激励:
l 人工激励,受人为因素影响严重;
l 设备简单,移动方便,不影响试件的动态特性;
l 快速地宽频带激励。
激振器激励:
l 难于安装,操作复杂,存在附加影响;
l 有多种激励信号可供选择,且激励信号已知;
l 经常用于大型复杂结构;
l 适当选择激励信号能改善线性结构的测量结果;
l 结构存在非线性时,选择适当信号既可以把非线性平均掉。
力 谱
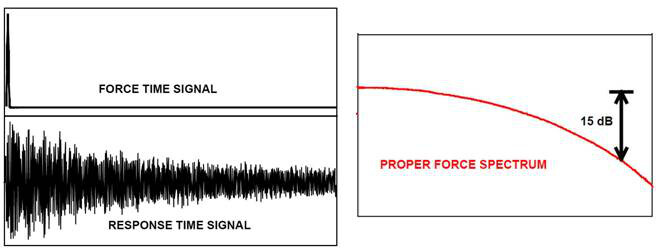
力脉冲的自谱
平 均
力锤法:每个测点位置锤击的次数
激振器法:激励信号重复激励次数
参 考 点、参 考 点 选 择 的 原 则
l 不能位于所关心的模态的节点上;
l 参考点处的振动量要显著;
l 先验知识、分析模型等;
l 选择多点作为参考点。
驱 动 点 (原点)、跨 点
驱动点:激励和响应在同一测点位置
跨点:激励和响应不在同一测点位置
驱动点测量具有一些重要的特征:
l 共振峰和反共振峰交替出现,这一点在FRF的幅值曲线图中得到体现;
l 每经过一个共振峰时相位滞后180度,每经过一个反共振峰时相位超前180度;
l 频响函数虚部的所有峰值都位于频率轴的同一侧。
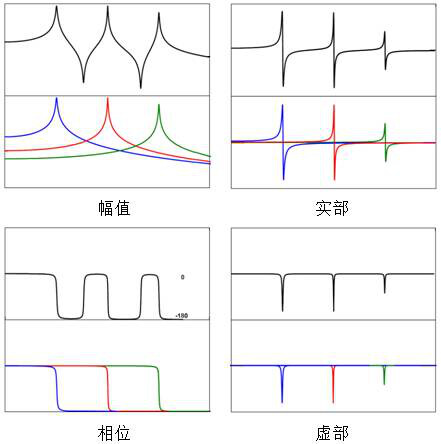
驱动点FRF(幅值、相位、实部和虚部)
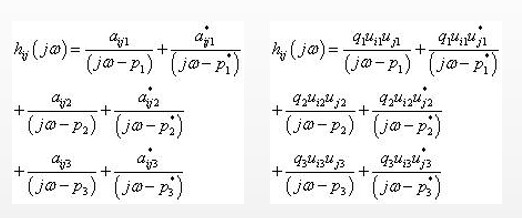
本文来自常州润田电子科技有限公司
来源:汽车NVH云讲堂