摘 要
本文介绍了在空气动力学设计计算方法和悬架设计分析方法的帮助下,为 SAE 级方程式赛车开发空气动力学套件和悬架系统的过程。空气动力学套件包括前翼和尾翼,悬挂系统包括带双叉臂的支柱式减震器。通过 FSAE 规则手册,确定了车辆参数,如轴距、宽度等以及前后翼板的几何形状。对各种几何配置下的高升力低雷诺数翼面进行二维 CFD 模拟,以选择具有最佳性能特征的翼面配置。根据二维模拟获得的数据制作前后机翼的三维模型,以便对机翼以及带机翼和不带机翼的整个汽车总成进行三维模拟。由于悬挂系统在汽车动力学中起着非常重要的作用,因此对悬挂系统进行了运动学分析。从空气动力学模拟和悬挂系统分析中获得的数据将在单圈时间模拟器中进行分析,以预测和比较安装和未安装空气动力学套件的汽车的性能和单圈时间。
01 前 言
空气动力学是一门研究空气与固体物体(如翼型)相互作用所产生的力和力矩的学科。当空气在翼型周围流动时,根据翼型的几何形状,主要会产生升力或下压力以及阻力。根据伯努利原理的解释,当翼型下方形成高压区时,由于气流在底部区域的速度较低,就会产生升力。同样,如果机翼的几何形状沿水平轴线倒置,则气流在底面的速度较高,而在上表面的速度较低。顶面的速度较低,从而在顶面形成较高的压力区,产生反方向的升力,这就是所谓的下压力。在过去的30-40年里,空气动力学一直是赛车运动中的一个重要课题,其唯一目的就是增加轮胎上的垂直力(下压力),从而在不增加车辆质量的情况下增加轮胎接触点的抓地力。抓地力的增加可提高赛车的性能,从而加快圈速。这一因素同样适用于FSAE级方程式赛车。FSAE方程式赛车的空气动力套件包括前翼、后翼和车身底部扩散器,它们相互配合以增加赛车的下压力。在设计敞篷赛车时,会遇到许多复杂的几何形状,如旋转车轮、A臂和带有驾驶员的驾驶舱等。由于赛车的这种性质,要想通过分析来解决整辆赛车的空气动力学设计问题,即使不是不可能,也肯定是很困难的。正是由于存在这些困难,在设计赛车的空气动力学套件时才采用了计算流体动力学(CFD)等模拟方法。除了空气动力学套件,车辆动力学对于FSAE赛车的性能也同样重要。赛车的动力性能决定了车辆的操控性,以及当驾驶员输入指令时,车辆在直道和弯道上的表现。空气动力套件可改善车辆的操控性。悬挂系统和转向系统决定了汽车的转弯半径、车轮的方向、汽车在三个轴上的表现,即X轴(滚动运动)、Y轴(俯仰运动)和Z轴(偏航运动)。本文旨在建立车辆动力学方面与空气动力学方面之间的相关性,以及它们如何共同作用以制造出性能更佳的汽车。本文的主要目的是为FSAE赛车设计和开发一套空气动力学套件,以提高赛车在单圈时间和加速度方面的性能。设计符合FSAE规则的空气动力学套件。在各种CFD模拟的帮助下,优化前翼和后翼的设计以及整车装配,以实现良好的空气动力效率(高升力和低阻力特性)和平衡。设计整套车辆动力系统,包括悬挂系统、转向系统和制动系统,以实现良好的车辆操控性和稳定性,从而间接提高赛车性能。在不同的FSAE赛道上,对所设计的赛车进行有无空气动力学套件的单圈时间模拟,以帮助量化本项目的成果。为提高加速、转弯和制动速度,对汽车的空气动力抓地力进行了探索。通过风洞试验和计算流体动力学(CFD)模拟,研究了原型后扰流板的空气动力升力。对不同攻角的实验数据和数值数据进行了并列分析。
02 仿真步骤
设计的空气动力装置,如前翼子板和后翼子板,被添加到整个车身中,并通过模拟来验证改进效果。前翼和尾翼被放置在FSAE 规则规定的适当位置上。对未安装空气动力学套件和安装了空气动力学套件的赛车进行了模拟,以显示赛车性能的提高,并证实空气动力学套件的使用。车头的离地间隙为 30 毫米,并考虑到悬挂系统在向下方向的最大行程为 25 毫米。如前几节所述,根据FSAE规则手册,翼片被放置在规定的位置上。带空气动力学套件和不带空气动力学套件的两种车辆设置如图 1 所示。

图 1:配备气动套件的车辆设置
在 Space Claim 中对汽车几何形状进行了修改,以简化车身并去除可能破坏网格的多余元素。模型中还添加了珀西(驾驶员)的虚构模型,因为驾驶员是影响方程式赛车阻力的关键因素。驾驶舱被密封,某些复杂的部分被简化。控制体积的横截面为 6000 毫米乘 6000 毫米,尾流为 9000 毫米,为了进一步简化模拟,我们沿对称面切割了控制体积,以节省计算时间和精力。我们添加了两个影响体,一个用于进一步细化网格,另一个用于加密尾流。在生成带有空气动力学套件的汽车网格时,我们注意到了网格干扰,并进行了微小的修改以提高网格质量。
网格划分是任何模拟中最重要的部分,因为模型的准确性取决于网格的性质。网格还影响计算能力和时间。需要在细化程度上达到完美平衡,这样不仅能生成精确的结果,还能节省时间和计算能力。为了在某些关键和复杂的几何形状上更好地细化网格,应用了各种局部尺寸。模拟生成的网格表面如图2所示。

图 2:表面网格
模拟初始化采用了带有曲率校正的 k-omega SST 湍流模型。空气相对速度为 27 米/秒。在本次模拟中,车身处于静止状态,空气和地面等所有其他部分相对于车身运动。在车轮网格中添加了 116 rad/s的旋转运动,在地面网格中添加了 27 米/秒的平移运动。
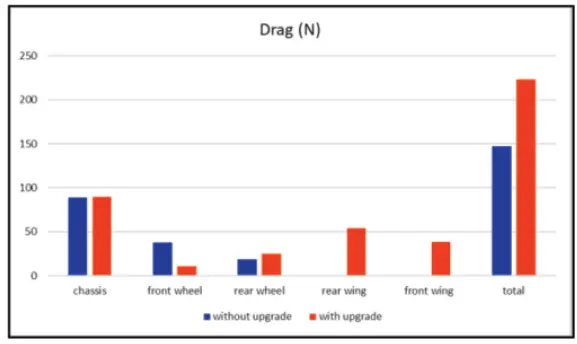
图 3:有无气动附件时作用在车辆各部件上的阻力
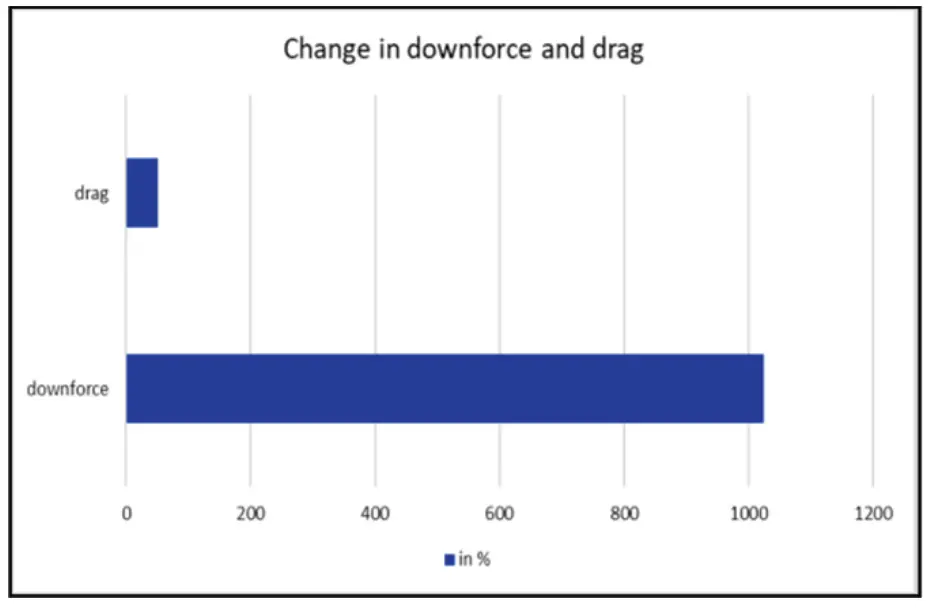
图 4:空气动力升级后作用在车辆上的下压力和阻力的百分比变化
我们成功地获得了仿真结果,可以推断出在性能方面取得了各种有益的改进。为了证明这一结论,我们获得了整套车辆和各个部件的升力系数、阻力系数、升力和阻力。
03 圈速模拟
通过单圈时间模拟,分析所设计的空气动力学套件对赛车性能的影响,即在特定赛道上的单圈时间和加速度。
本项目中所有圈速模拟使用的软件都是OptimumLap。它是由OptimumG公司开发的一款开源软件,该公司由最负盛名的FSAE裁判ClaudeRouelle先生于1978年创立。
OptimumLap是一款简化的车辆模拟工具,用于估算车辆在特定赛道上的性能。在该软件中,车辆被简化为最基本的组件,因此只需10个参数就能定义车辆,每个参数代表汽车的一个特定方面,如发动机、轮胎和空气动力学,这样就能轻松查看每个参数对车辆性能的影响。
OptimumLap中使用的车辆模型是一个点质量准稳态模型。从数学角度看,这种方法过于简单,但实际上,这种模型在分析车辆的整体性能趋势和比较以下方面非常强大:研究人员无需捕捉或仿真更详细的影响,就能研究车辆不同配置之间的性能。它的工具使研究人员能够研究空气动力学套件、轮胎和悬挂系统以及质量的影响。
仿真过程第1步:通过输入各种空气动力、车辆动态和动力装置参数,如质量、驱动车轮、轮胎半径、空气动力系数(升力和阻力系数)和动力装置扭矩-转速数据,建立车辆模型。第2步:这一步涉及赛道建模,赛道建模有两种方法,一种是从OptimumLap数据库中直接导入已有的赛道,另一种是通过输入直线段长度和转角半径来建模自定义赛道。第3步:通过选择相应的车辆和赛道模型来运行模拟,并在模拟完成后提取所需数据。
仿真输入参数如前所述,模拟是针对汽车的两种配置设置进行的,即不带空气动力学套件的汽车和带空气动力学套件的汽车,因此会有两套汽车模型和输入参数。不过,由于两辆车都采用相同的动力传动系统,因此动力传动系统的输入参数将保持不变。升力和阻力系数、正面面积和空气密度等空气动力参数来自前几章所述的CFD模拟。车辆动态和动力传动系统参数,如车辆质量、轮胎半径、摩擦系数和电机扭矩-转速数据,来自方法论中提到的初始设计考虑因素,以及悬架设计和分析所获得的结果。配置2:带空气动力套件(表2)。
仿真装置参数如方法论中所述,动力系统中使用的电机是名为Emrax-188的轴向磁通电机。图5显示了电机的扭矩、功率和转速(速度)数据,这些数据被用来为当前模拟的车辆建模。
表 1:配置 2 的输入参数
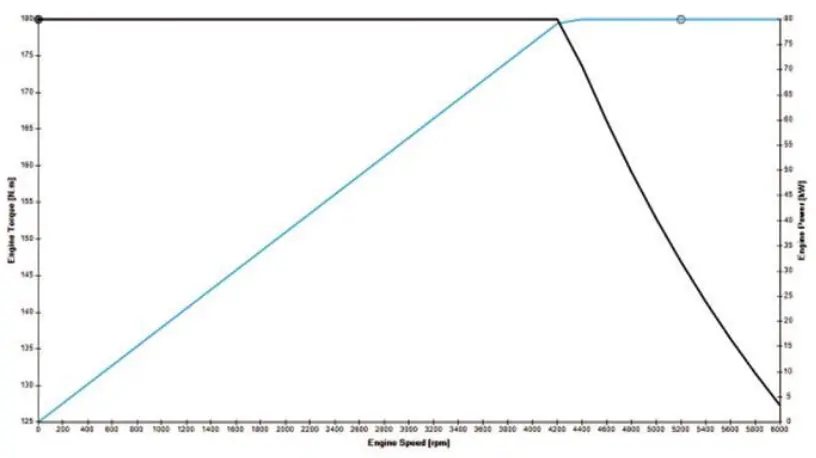
图 5:电机功率 v/s 扭矩曲线
首先,对模拟获得的两种配置赛车的牵引力模型进行比较和分析,然后将模拟生成的单圈时间、横向和纵向加速度、速度图和其他各种数据列表,并对每条赛道 进行分析。
04 牵引模式
图 6 显示了配置 1 的模拟牵引模型,即没有空气动力套件的汽车。图中黑线表示作用在车轮上的驱动力(电机产生的扭矩),或者换句话说,作用在车轮上的牵引力。绿线代表牵引力极限或轮胎支持的最大牵引力,取决于可用的摩擦抓地力作用在车辆和轮胎上的正常负载(空气动力下压力)。阴影区域被称为牵引力受限区域,在该区域内,由于摩擦抓地力不足,汽车无法完全利用动力装置(电机)产生的驱动力。
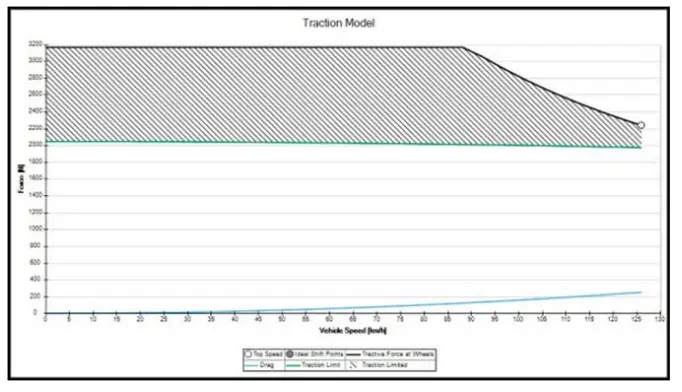
图 6:配置-1 的牵引模型
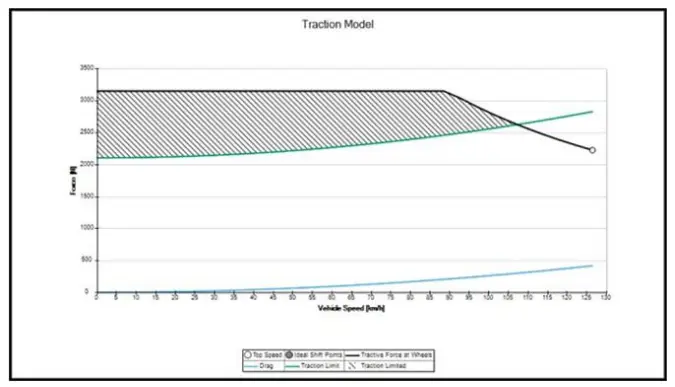
图 7:配置 2 的牵引模型
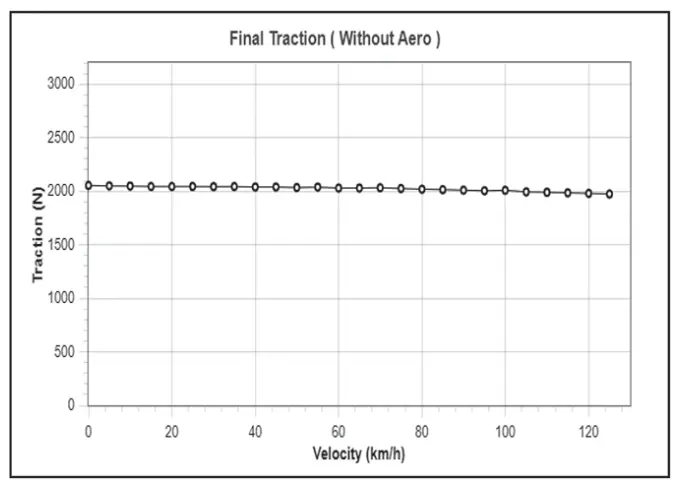
图 8:配置-1 的最终牵引力曲线
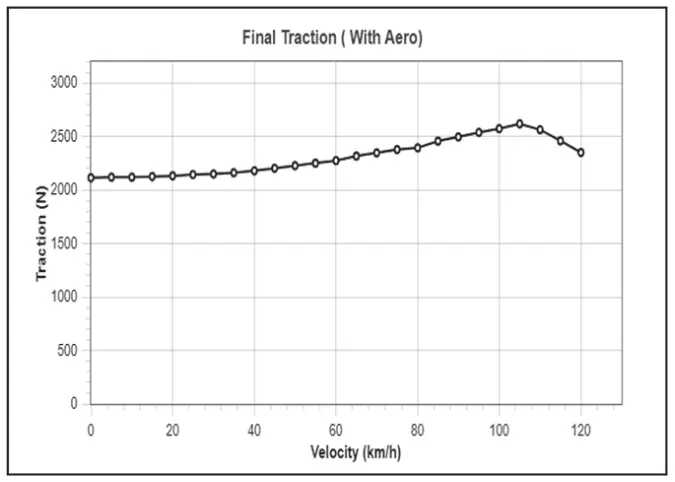
图 9:配置-2 的最终牵引力曲线
因此,从上图数据中我们可以看出,汽车配置 1 受牵引力限制。从上述配置 2 的牵引力模型数据可以看出,随着空气动力套件的使用,牵引力在各方面,即最大牵引力、最小牵引力和平均牵引力都有所提高。
05 结论
• 配置 1(无气动套件),在速度为 97.2 km/h 时,阻力为 294.7 N,升力为 91.82 N。
• 配置 2(带气动套件)在速度为 97.2 km/h 时获得了446.38 N 的阻力和-848.9576N 的升力(向下力)。
• 增加的空气动力装置,如前后翼和车底扩散器,大大提高了车辆的下压力水平。这些改进将提高车辆的牵引能力和转弯速度。这可以通过在各种赛道上进行的单圈时间模拟来推断。
• 通过对FSAE赛车实施空气动力学套件,在牵引力模型中观察到以下趋势:平均牵引力增加了328.883N。最高可用牵引力增加了 761.468N。平均时速60 公里时的牵引力增加了 237.697N。
来源:AutoAero