1. 爆胎力学特性分析
车辆爆胎时,会导致其爆胎轮胎力学特性和车辆运动状态发生大幅度变化,主要变化的是侧偏刚度参数、回正力矩大小、径向刚度参数、侧倾刚度参数、纵滑刚度参数、滚动阻力系数和有效滚动半径的大小。考虑到轮胎爆胎实验的所需要的时间较长、轮胎爆胎时具有高危险性和实现轮胎爆胎的场地要求高等因素,本文基于已公开的爆胎实验数据建立四轮分布式驱动汽车爆胎模型。因为轮胎发生爆胎和结束的时间是极短的(一般为0.1秒),在爆胎过程中很难得出车轮胎压与其力学特性的变化规律,所以为了简化分析,假设爆胎过程中车轮的力学特性参数变化都是理想的线性变化的。
车辆在运动时,轮胎的有效滚动半径是在一定的正常范围内波动的。目前主要是通过有效滚动半径的经验公式来表示有效滚动半径,公式如下:
式中,Rc为有效滚动半径;Rn为自由半径;Rt为静态负载半径。
车轮爆胎后车轮的胎压会在短时间内减小,从而导致有效滚动半径也会在短时间内减小,车轮爆胎后其有效滚动半径会在短时间内减小到正常大小的70%(与轮胎型号有关)。假设爆胎过程中车轮的有效滚动半径是理想的线性变化,则可得在在爆胎过程中,车轮的有效滚动半径的表达式为:

式中,t0为车轮发生爆胎的起始时间点;td为爆胎持续时间(一般为0.1s左右);Rc0为爆胎前的有效滚动半径。
根据公开的爆胎实验数据可知,不考虑轮胎脱落和轮辋触地等情况,车轮爆胎后其侧偏刚度会急剧减小,随后逐渐趋于稳定。假设爆胎过程中轮胎的侧偏刚度是理想的线性变化,则可得在爆胎过程中,侧偏刚度的表达式为:
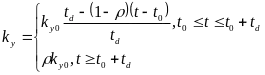
式中,ky0为爆胎前的侧偏刚度;ρ为爆胎后侧偏刚度的衰减系数,一般可取0.2~0.3。
根据车轮爆胎力学特性分析,整理车轮爆胎参数变化过程,如图1所示。
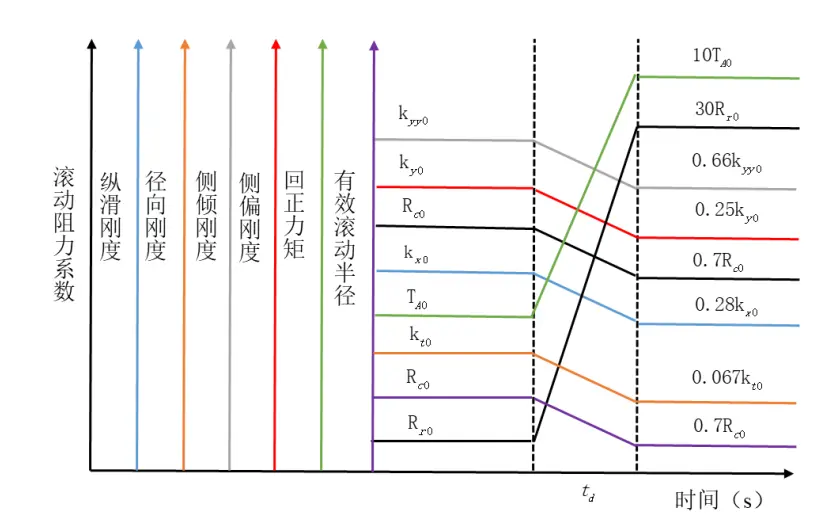
图1 车轮爆胎参数变化
2. 爆胎稳定性仿真分析
车辆发生爆胎后,车辆的动力学变化会受到各种外部环境和内部条件的影响,例如车轮爆胎的位置、驾驶员的干扰程度和当前的路面状况等。所以为了更全面地实现车辆爆胎的稳定性控制,利用carsim和simulink进行联合仿真分析。
在直行工况下,以车辆左前轮爆胎为例进行分析,车辆各个轮胎力变化如下图所示。
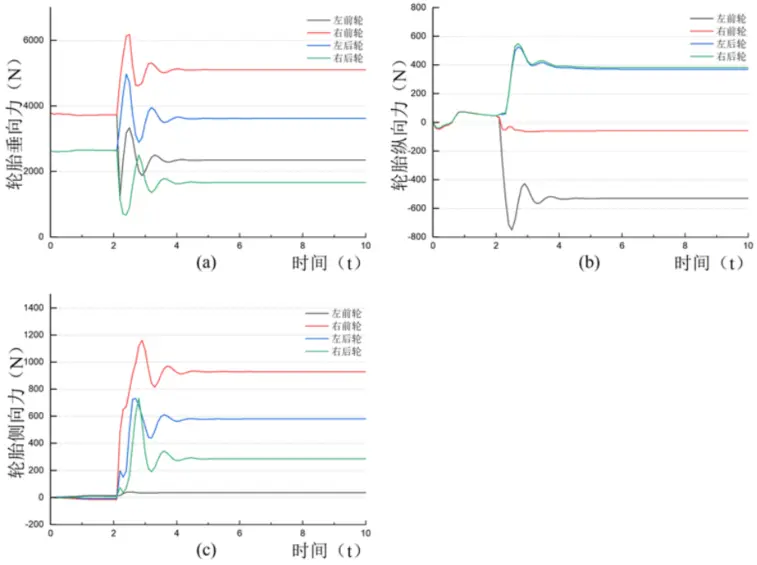
图2车辆左前轮爆胎动力学变化
由图2(a)可知,车辆左前轮发生爆胎时,爆胎车轮的径向刚度在短时间内降低,同时爆胎轮胎的有效滚动半径减小导致悬挂高度发生变化,进而影响车辆的垂向平衡,导致轮胎的垂向力发生变化,其中左前轮和右后轮的垂向力急剧减少,而右前轮和左后轮的垂向力在短时间内增大。由图2(b)可知,由于车轮爆胎时,爆胎轮胎的滚动阻力急剧增大为正常轮胎的三十倍,导致爆胎轮胎产生较大的制动力,且左前轮产生的反方向的纵向力远大于右前轮的纵向力,进而产生逆时针方向的附加横摆力矩。由图2(c)可知,由于车辆爆胎时,爆胎轮胎的侧偏刚度急剧降低以及轮胎的有效滚动半径减小,导致爆胎车辆的右前轮、左后轮和右后轮的侧向力急剧增大,且方向均向左,同时产生了逆时针方向的附加横摆力矩,与轮胎纵向力产生的附加横摆力矩叠加,从而导致车辆向左侧偏航。
当车辆左后轮爆胎为例进行分析,车辆各个轮胎力变化如下图所示。
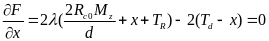
图3 车辆左后轮爆胎动力学变化
由图3(a)可知,车辆的左后轮爆胎后,由于爆胎轮胎的径向刚度有所降低,左后轮的轮胎垂向力急剧减小,同时由于车轮轮心高度和轮胎的有效滚动半径发生变化,导致各车轮的垂向力重新分配,其中,左前轮和右后轮的垂向力急剧增大,而右前轮的垂向力有所减小。由图3(b)可知,由于车辆爆胎轮胎产生的滚动阻力,左后轮产生反方向的纵向力,且远大于车辆的右后轮,进而产生一个逆时针方向的附加横摆力矩。由图3(c)可知,车辆的左后轮爆胎后,由于侧偏刚度和轮心高度的变化,没发生爆胎的轮胎首先产生向右的侧向力,但是在短时间内向左急剧增大,各车轮的垂向力重新分配完成后趋于稳定,同时产生一个顺时针方向的附加横摆力矩,考虑车辆前后轴距的大小,各轮胎侧向力产生的附加横摆力矩大于纵向力产生的横摆力矩,有一部分横摆力矩相互抵消后,车辆会向右侧偏航。
综上所述,在直行工况下,车辆前轮发生爆胎时,更容易造成二次事故。因为车辆前轮爆胎时车辆的状态参数变化幅度都远超过了后轮爆胎,且相关状态参数达到稳定不变的时间更慢,即爆胎后轮胎的动态过程持续时间更长。当车辆发生爆胎时,各车轮的所受到的垂向力会产生变化,且车轮爆胎的阻力急剧变大,从而导致车辆产生侧偏现象,且在相同的情况下前轮爆胎后导致的侧向偏移程度更大。同时车辆的后轮爆胎时,车辆的偏航方向取决于各轮胎侧向力和纵向力所产生的附加横摆力矩叠加的大小和方向,而不同车型的前后轴距和轮距都可能存在差异,所以车辆后轮爆胎时偏航的方向是不确定的。其次,车辆爆胎时,由于有效滚动半径的减小,车辆悬挂高度也会因此降低,从而导致车身侧倾,所以车身会在短时间内出现上下震荡现象,这与车辆实际的爆胎情况一致,更一步证明了车辆爆胎动力学仿真模型的准确性。
3. 二自由度动力学模型车辆爆胎稳定性控制的主要目的防止车辆在爆胎后陷入失稳状态。为了确定汽车是否处于稳定状态中,需要分析汽车相关运动状态的变化和车辆稳定状态之间的联系,而横摆角速度可以间接地反映出车辆的稳定状态,同时质心侧偏角在一定的范围内也能直接反映出车辆是否已经处于失稳状态。为了更好地分析汽车爆胎后的稳定性和运动状态变化,忽略转向系统、悬挂系统和各种环境因素等影响,假设车辆在最理想的状态下运动,不考虑车辆的侧倾运动,建立爆胎前的二自由度理想车辆模型如图4所示:
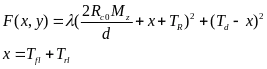
图4 二自由度理想车辆模型
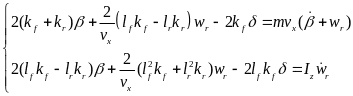 (1)
(1)
式中,kf和kr分别为前后轮的侧偏刚度;ꞵ为质心侧偏角;lf为质心到前轴的距离;lr为质心到后轴的距离;wr为横摆角速度;δ为前轮转向角;vx为纵向速度,Iz为转动惯量;L为前后轴的距离。
车轮爆胎后其侧偏刚度会急剧减小,减小为原来的ρ倍左右并逐渐稳定。因此,以左前轮发生爆胎为例,发生爆胎后的二自由度模型将迁移为如下形式:
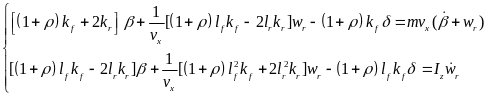 (2)
(2)
相类似的,以左侧两个轮胎爆胎为例,发生爆胎后的二自由度模型为:
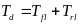
4. 目标横摆角速度和质心侧偏角
由于车辆各个轮胎力大小不同,对车辆质心产生横向的力矩从而产生了横摆角速度,会对车辆的运动状态产生影响,所以可以间接地反映车辆是否处于稳定的状态下。车辆稳态行驶时,横摆角加速度为零,即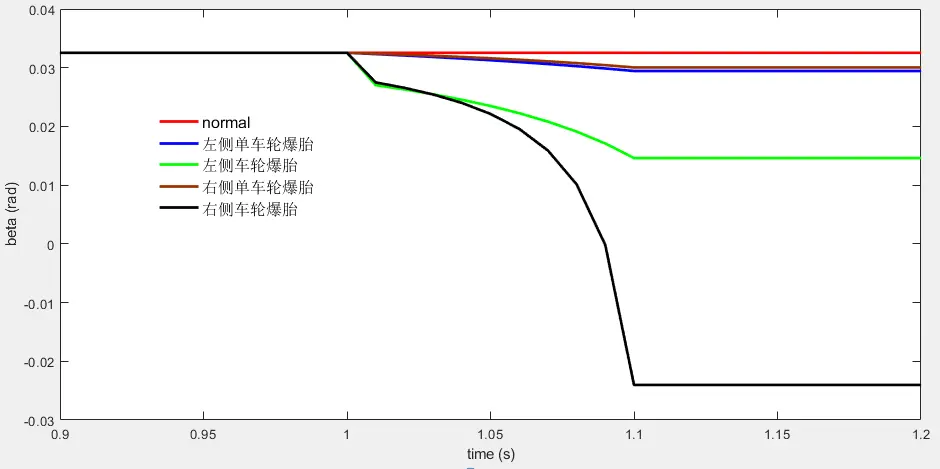 ,车辆的侧向加速度也为零,即
,车辆的侧向加速度也为零,即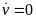 ,则代入式(2)中得:
,则代入式(2)中得:
 (3)
(3)
根据式(3)中的第二个等式可得:
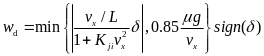 (4)
(4)
将上式带入式(3)中的第一个等式化简可得车辆稳定时的横摆角速度为:

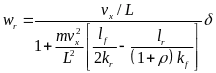 (5)
(5)
将式(5)带入(4)中可得车辆稳定时的质心侧偏角为:
 (6)
(6)
车辆正常行驶时的稳定性因数Knormal如下:
 (7)
(7)
由式(5)可得左前轮爆胎后的稳定性因数为:
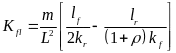 (8)
(8)
所以,车辆处于稳态时的横摆角速度和质心侧偏角可以用下式表达:
 (9)
(9)
相类似的,可以得到左后轮爆胎后的横摆角速度和质心侧偏角稳态响应特性为:
 (10)
(10)
当单侧两个轮胎爆胎后,横摆角速度和质心侧偏角稳态响应特性为:
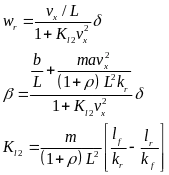 (11)
(11)
其中,Kji为车轮ji发生爆胎后的稳定性因数。由上式进而可以得到当轮胎爆胎后稳定性因数的变化规律。
假设在1s时左侧轮胎发生爆胎,车速为5m/s,前轮转角为5deg,根据carsim中仿真模型车的参数值可以得到如下图所示的爆胎稳定性因数、横摆角速度和质心侧偏角的对比图。
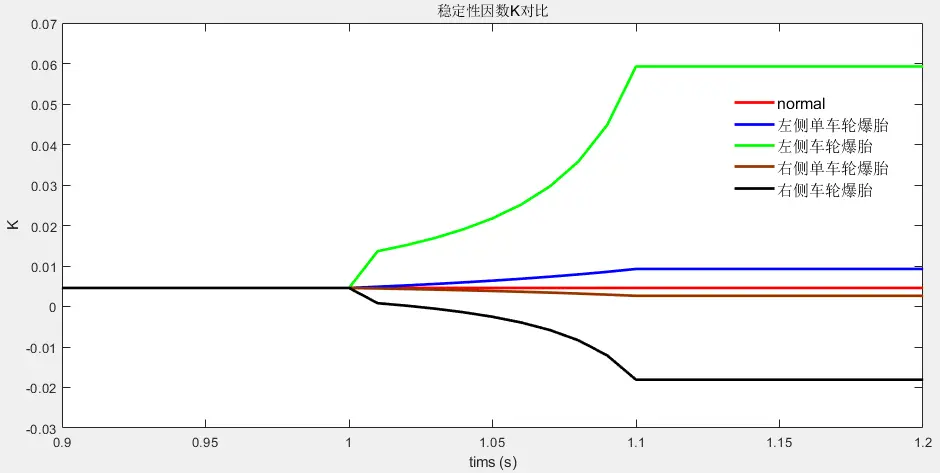
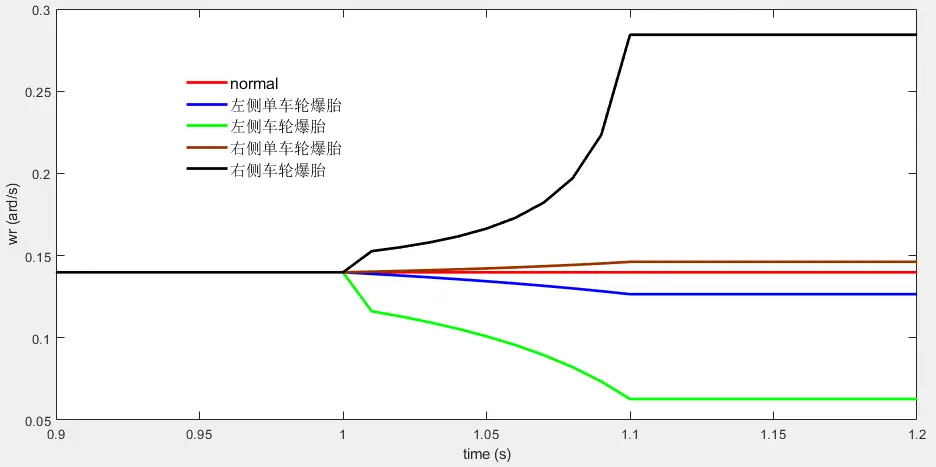

图5 爆胎后稳态响应的变化图
当左侧车轮发生爆胎时,横摆角速度在td时间内逐渐变小,质心侧偏角在td时间内逐渐变大;当右侧车轮发生爆胎时,横摆角速度在td时间内逐渐变大,质心侧偏角在td时间内逐渐变小。当左侧前后轮都爆胎后稳定性因数的值变大,加剧了汽车的不足转向特性(K>0);当右侧前后轮都爆胎后稳定性因数的值变为负数,将原本车的不足转向特性变为过度转向特性(K<0)。
路面附着系数的大小会对车辆的横摆角速度产生影响,车辆的横摆角速度极限值为:
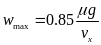 (12)
(12)
所以车辆在稳定的状态下,理想的横摆角速度为:
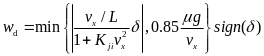 (13)
(13)
路面附着系数的大小会对车辆的质心侧偏角产生影响,车辆的质心侧偏角极限值为:
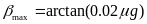 (14)
(14)
所以车辆在稳定的状态下,理想的质心侧偏角为:
 (15)
(15)
目前,大部分的车辆爆胎纵向稳定性控制策略都是通过车辆制动来实现,基于四驱分布式驱动汽车合理地对四个电机进行驱动扭矩矢量控制,实现汽车的纵向爆胎稳定性控制的研究较少。考虑到在高速工况下车辆爆胎时进行紧急刹车时,容易造成二次事故,尤其是雨雾天气时,路面湿滑以及能见度较低,更容易造成追尾事故。本章针对四轮分布式驱动汽车提出纵向爆胎稳定性控制策略,以实现爆胎车辆的稳定性控制。纵向爆胎稳定性控制策略的结构如图6所示。
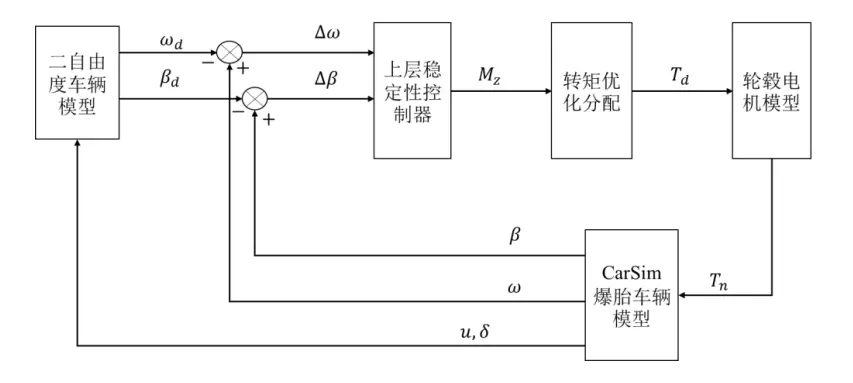
图6纵向爆胎稳定性控制策略结构
加入附加横摆扭矩Mz后动力学模型变为:
 (16)
(16)
运动控制器通过相关的控制算法控制车辆保持在期望的运动状态下,实时求解出整车的需求横摆力矩进行驱动或制动控制,以保证爆胎车辆稳定运行。运动控制器主要包括两部分:
首先是车辆运动状态稳定变量的选取。车辆对目标路径的跟踪效果以及车辆运动时的稳定性,主要是间接通过车辆横摆角速度的大小来表征,而质心侧偏角大小可以更直观地体现车辆跟随目标轨迹的能力。
其次是确定合适的目标跟踪算法。目前应用于车辆稳定性控制算法相对较多,本文采用pid算法设计上层稳定性控制器。
定义横摆角速度和质心侧偏角误差如下:
 (17)
(17)
总误差为:
 (18)
(18)
其中,k为横摆角速度误差项所占的比例系数。
则附加横摆扭矩可通过下式得到:
 (19)
(19)
其中,kp,ki和kd分别为比例项,积分项和微分项的比例因子。
对Mz做出限制:
 (20)
(20)
转矩分配策略需要充分考虑车辆爆胎时轮胎的力学特性、路面附着系数和电机转矩峰值等约束条件下,将上层横摆力矩控制器得到的期望的横摆力矩进行分配。对于爆胎车辆的附加横摆力矩分配问题,目前的研究大部分采用简单的分配方式,即在车辆的轮胎爆胎一侧增加驱动力或减少制动力,相应地在另一侧减少驱动力或增加制动力,以实现爆胎车辆的稳定性控制,但是在实际的应用中,可能会受到道路、天气和车辆自身等影响,稳定性控制应具有良好的适应性和响应速度。所以本文根据四轮分布式驱动汽车的四个车轮转矩可以独立控制的特性,同时考虑道路变化、天气变化和执行器性能等约束条件,并利用各个轮胎所受的垂直负载变化,对期望横摆力矩做出合理分配。
车辆发生爆胎时,爆胎车轮相邻的轮胎垂直载荷均有所增加,且同一侧的增加量相对较大,同时爆胎车轮与斜对角车轮的垂直载荷均有所下降,所以为了抵消车辆爆胎产生的附加横摆力矩同时维持车辆的行驶速度,因此根据车辆垂直载荷的转移变化,对驱动力进行重新分配,根据垂直载荷的变化量提高爆胎车轮相邻驱动轮的驱动力,降低爆胎车轮与斜对角车轮的驱动力。由于车辆爆胎是涉及车辆自身条件、路面条件和驾驶员等因素的复杂工况,所以车辆爆胎后所产生的影响以及车辆爆胎时车辆的运行状态、轮胎爆胎的原因和轮胎爆胎后轮胎的状态变化等也会存在差异性,因此无法全面考虑车辆爆胎后的情况。本文假设车辆爆胎后,当驱动轮均能正常工作时,采取车辆爆胎纵向稳定性控制策略,避免车辆爆胎后因为紧急制动或停留在行驶车道上而造成二次追尾事故。基于动态垂直载荷的转矩分配策略结构框图如下图所示。

图6 动态垂直载荷转矩分配策略结构框图
6.1 爆胎前
假设车辆的总扭矩为Td,则有:
 (21)
(21)
式中,Tfl、Tfr、Trl、Trr分别为四个车轮的转矩。
四个电机产生的转矩需要满足整车直接横摆力矩控制要求,即:
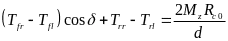
其中,d为轮距,Rc0为爆胎前的有效滚动半径,可假设四个轮胎的有效滚动半径相同。
假设前轮转角非常小,则cosδ≈1,则扭矩差动转向方程为
 (22)
(22)
车辆运行时,车辆的前后载荷为:
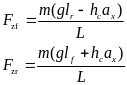 (23)
(23)
通过前后轴垂直载荷分配的直接横摆力矩为:
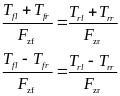 (24)
(24)
联合以上公式,可化简得分配到四个电机的转矩为:
 (25)
(25)
6.2 爆胎稳定过程中
当轮胎发生爆胎且车辆动力学状态还未稳定之前,此时爆胎的车轮是还需要施加扭矩的,等车辆稳定之后,爆胎的车轮将不再施加扭矩,该过程持续时间较短。
总的驱动扭矩为
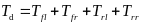
假设前轮转角较小,则扭矩差动产生的附加横摆扭矩Mz为
 (26)
(26)
其中,Rij为各轮胎的有效滚动半径,由于轮胎胎压的快速损失,从而导致轮胎的有效滚动半径也会迅速减小,因此,爆胎后各车轮的滚动半径不尽相同。
与爆胎前的场景相类似,联立式(21)、(22)、(23)、(24)和(25),可得四个驱动电机的转矩为:
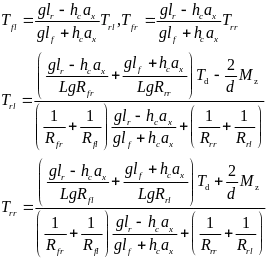 (27)
(27)
当四个轮胎均为爆胎时,各轮胎的有效滚动半径都相同即Rc0,代入上式可得扭矩分配策略(25)。
6.3爆胎稳定后
当轮胎发生爆胎且车辆稳定之后,或者爆胎的轮胎发生胎面剥落,此时爆胎的车轮是不能施加扭矩的。
轮胎垂向力计算公式:
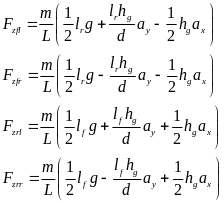 (28)
(28)
其中,hg为质心高度。
6.3.1 单个轮胎爆胎
(1)左前轮发生爆胎
当左前轮不施加驱动扭矩时,此时扭矩分配的公式变为:
 (29)
(29)
通过上述公式可以得到另外几个轮胎的驱动扭矩分配如下:
 (30)
(30)
(2)右前轮发生爆胎
当右前轮不施加驱动扭矩时,此时扭矩分配的公式变为:
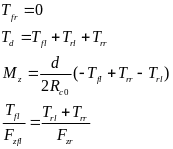 (31)
(31)
通过上述公式可以得到另外几个轮胎的驱动扭矩分配如下:
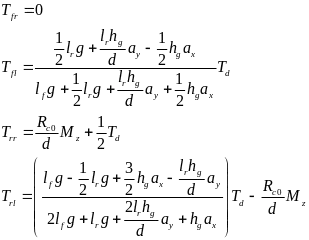 (32)
(32)
(3)左后轮发生爆胎
当左后轮不施加驱动扭矩时,此时扭矩分配的公式变为:
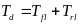 (33)
(33)
通过上述公式可以得到另外几个轮胎的驱动扭矩分配如下:
 (34)
(34)
(4)右后轮发生爆胎
当右后轮不施加驱动扭矩时,此时扭矩分配的公式变为:
 (35)
(35)
通过上述公式可以得到另外几个轮胎的驱动扭矩分配如下:
 (36)
(36)
6.3.2 两个轮胎爆胎
仅考虑左侧或右侧两个轮胎同时爆胎的情况,此时需考虑爆胎后轮胎的滚动阻力。
(1)左侧两个轮胎发生爆胎
当左侧车轮不施加驱动扭矩时,此时扭矩分配的公式变为:
 (37)
(37)
其中,TR为左侧爆胎轮胎的滚动阻力。则要在满足上面两个公式的前提下,尽量满足下面等式:
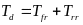 (38)
(38)
利用最小二乘法,构造目标函数:
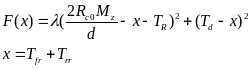 (39)
(39)
其中,λ是权重系数,为了优先保证车辆侧向稳定性,因此λ>>1。对目标函数求偏导数并使其为0:
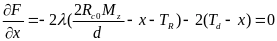 (40)
(40)
可得:
 (41)
(41)
由上式可见,最终的驱动扭矩由目标驱动扭矩和目标横摆扭矩共同决定,且横摆扭矩的优先级更高。
通过上述公式可以得到几个轮胎的驱动扭矩分配如下:
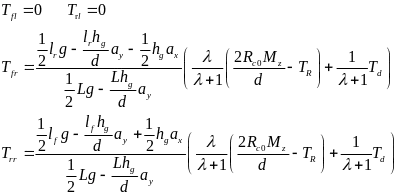 (42)
(42)
(2)右侧两个轮胎发生爆胎
当右侧车轮不施加驱动扭矩时,此时扭矩分配的公式变为:
 (43)
(43)
则要在满足上面两个公式的前提下,尽量满足下面等式:
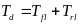 (44)
(44)
与左侧轮胎爆胎场景相类似,构造目标函数:
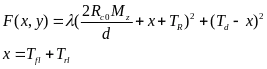 (45)
(45)
对目标函数求偏导数并使其为0:
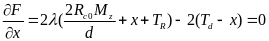 (46)
(46)
求解可得:
 (47)
(47)
由上式可见,最终的驱动扭矩由目标驱动扭矩和目标横摆扭矩共同决定,且横摆扭矩的优先级更高。
通过上述公式可以得到几个轮胎的驱动扭矩分配如下:
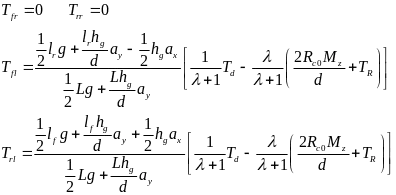 (48)
(48)
来源:智能运载装备研究所












