电动非承载式汽车车架作为电动汽车的重要部件，由于其在工作时承受了大部分整车部件的质量，因此车架将产生一定程度的弯曲与扭转变形。并且，来自不平路面的激励也将通过轮胎、减振器、钢板弹簧等部件传递到车架上。在车辆实际行驶过程中，车架所需的性能包括模态性能、刚度性能、强度性能和疲劳性能，这些性能对整车的安全性、操纵稳定性、舒适性和可靠性具有重要影响。因此，车架必须拥有良好的结构性能，其性能的好坏直接影响整车综合品质的优劣。本章将基于第 2章建立的有限元模型和多体动力学模型，完成对电动汽车车架各个性能的有限元分析。分析结论将为后续的电动汽车车架结构优化工作打下基础，电动汽车车架的各性能仿真值将为优化分析提供参考。
注：本文节选自《新能源汽车车架设计 结构性能与多目标协同优化研究》，由机械工业出版社出版
本书适用于对新能源汽车结构设计及优化技术感兴趣的读者，包括开发人员、设计人员、科研工作者等。本书还适用于有相关知识背景的从业人员。
《新能源汽车车架设计 结构性能与多目标协同优化研究》目录
前言
第1章 绪论1
1.1 新能源汽车行业发展概述1
1.2 国内外相关研究现状4
1.2.1 车架优化研究5
1.2.2 车架性能研究6
1.2.3 多目标优化研究8
1.3 研究价值分析11
1.4 主要内容概述11
1.4.1 主要研究内容11
1.4.2 主要分析内容12
第2章 多体动力学模型的建立与验证13
2.1 整车多体动力学模型建立的理论基础13
2.2 基础车前悬架多体动力学模型建立与验证15
2.2.1 基础车前悬架多体动力学模型的建立15
2.2.2 基础车前悬架多体动力学模型的验证17
2.3 基础车后悬架多体动力学模型建立与验证20
2.3.1 基础车后悬架多体动力学模型的建立20
2.3.2 基础车后悬架多体动力学模型的验证21
2.4 基础车多体动力学模型建立与验证22
2.4.1 基础车车架柔性体的建立22
2.4.2 基础车多体动力学模型的建立28
2.4.3 基础车多体动力学模型的验证29
2.5 电动汽车多体动力学模型的建立32
2.5.1 电动汽车动力学模型的建立32
2.5.2 电动汽车强度载荷分解多体动力学模型的建立33
2.5.3 电动汽车疲劳载荷分解多体动力学模型的建立34
2.6 本章小结34
第3章 电动汽车车架结构性能的研究35
3.1 电动汽车车架模态性能分析35
3.2 电动汽车车架刚度性能分析与对比36
3.2.1 基础车车架弯曲刚度分析37
3.2.2 基础车车架扭转刚度分析38
3.2.3 电动汽车车架刚度性能分析40
3.3 电动汽车车架强度性能分析40
3.3.1 电动汽车车架强度载荷的获取40
3.3.2 电动汽车车架强度分析方法44
3.3.3 电动汽车车架静态工况强度分析48
3.3.4 电动汽车车架制动工况强度分析50
3.3.5 电动汽车车架上跳工况强度分析52
3.3.6 电动汽车车架转弯工况强度分析54
3.3.7 电动汽车车架转弯制动工况强度分析56
3.3.8 电动汽车车架后制动工况强度分析58
3.3.9 电动汽车车架车轮上抬工况强度分析60
3.4 电动汽车车架路谱疲劳性能分析62
3.4.1 疲劳累计损失理论62
3.4.2 疲劳分析方法63
3.4.3 材料疲劳参数的确定63
3.4.4 道路谱载荷的采集67
3.4.5 疲劳载荷循环次数的确定73
3.4.6 电动汽车车架疲劳载荷的获取78
3.4.7 电动汽车车架疲劳性能的分析81
3.5 本章小结82
第4章 电动汽车车架多目标优化83
4.1 电动汽车车架参数化建模84
4.1.1 网格变形技术84
4.1.2 参数化模型的建立84
4.2 电动汽车车架多目标优化91
4.2.1 试验设计方法91
4.2.2 设计变量的选择分析94
4.2.3 优化问题的定义101
4.2.4 近似模型的建立方法102
4.2.5 近似模型的误差分析105
4.2.6 多目标优化分析108
4.3 电动汽车车架优化前后性能对比分析111
4.3.1 模态性能对比分析111
4.3.2 刚度性能对比分析112
4.3.3 强度性能对比分析113
4.3.4 疲劳性能对比分析116
4.3.5 质量属性对比分析117
4.4 本章小结118
第5章 电动汽车车架试验验证119
5.1 车架台架试验验证119
5.1.1 模态试验119
5.1.2 刚度试验120
5.2 整车道路耐久试验验证123
5.2.1 试验准备123
5.2.2 试验方法123
5.2.3 试验结果125
5.3 本章小结127
第6章 总结与展望128
6.1 总结128
6.2 主要研究价值129
6.3 研究成果的拓展129
6.4 未来技术发展分析130
6.4.1 模块化车架的设计130
6.4.2 新材料的应用130
6.4.3 新技术的融合131
参考文献133
3.4 电动汽车车架路谱疲劳性能分析
3.4.1 疲劳累计损失理论
若结构件承受的应力值超过了其疲劳极限值，则每一次循环都会形成损伤，损伤逐渐累积。如果每一次恒幅载荷循环的损伤为 1/N，则经历 n次循环的损伤为 Cn/N。变幅载荷循环的损伤不一样，每一次损伤累积则为其总损伤 D
式中，k为变幅载荷的应力水平；ni为在第 i级载荷下对应的循环次数；Ni为在第 i级载荷下对应的疲劳寿命。
当累积损伤达到临界时，结构件则会发生失效。对于实际工程中的疲劳问题，通常采用线性疲劳累积 Miner理论进行分析 [136]，其基本思想为：在载荷作用下，若结构件吸收的能量达到上限，则会发生疲劳破坏。假设在某一载荷作用下，结构件发生疲劳失效时的总循环次数为 N，吸收的能量为 W。结构件在受到 ni次循环载荷作用时，其吸收的能量为 Wi，则结构件吸收的能量 Wi与其循环次数 ni存在一定的线性关系，即
式（3-33）为 Miner线性累积损伤理论，当累积损伤之和达到 1时，结构发生疲劳破坏。ni为在 Si载荷下对应的循环次数，其可以通过载荷谱获取；Ni为在Si载荷下对应的疲劳寿命，其可以通过 S-N曲线或 ε-N曲线获取。Miner线性累积损伤理论的分析精度较高，目前广泛应用于实际工程开发设计中 [137]，因此本书采用该理论对电动汽车车架进行疲劳性能分析。
3.4.2 疲劳分析方法
基于有限元方法对寿命进行预测，在工程中运用得越来越广泛。常见的疲劳预测方法很多，按疲劳裂纹形成寿命预测的基本假定和控制参数，可以分名义应力法和局部应力- 应变法、裂纹扩展法。裂纹扩展法首先假定零部件内部存在初始裂纹，应用线弹性断裂力学方法来估算剩余寿命 [138]。此方法在航空领域应用较为广泛，汽车行业一般不采用该方法预测寿命。名义应力法是以结构的名义应力为试验和寿命估算的基础，采用雨流法压缩出，相互独立、互不相关的应力循环，结合实测的材料的 S-N曲线，按线性累积损伤理论预测结构件寿命的方法 [139]。该方法适用于弹性应力应变的高周疲劳及无缺口结构的应力寿命预算分析。
按疲劳寿命大小，可分为高周疲劳和低周疲劳。根据疲劳设计经验理论，一般以 105次寿命为界限；寿命小于 105次，定义为低周疲劳，寿命大于 105次，定义为高周疲劳。根据车架的使用寿命，车架疲劳通常不属于高寿命零部件。同时车架结构设计复杂，考虑加工工装固定、定位及涂装，以及支架安装，车架上开孔较多，在车辆运动过程中，极易在局部缺口处发生塑性变形，形成损伤。局部应力- 应变法解决了高应变的低周疲劳和带缺口结构的寿命预测问题，所以本书在对电动汽车车架的疲劳分析中，采用局部应力- 应变法对车架结构进行有限元分析，估算疲劳寿命。
局部应力- 应变法利用局部应变作为主要疲劳参数，基于材料的应力- 应变（-）曲线和应变- 寿命（ε-N）曲线，考虑缺口处的局部塑性变形的因素，对照塑性应变发生的情况，结合疲劳损伤预测理论，计算疲劳寿命的分析方法 [150]。局部应力- 应变法主要解决了高应变的低周疲劳和带缺口结构的寿命预测问题。同时考虑了加载顺序的作用和循环载荷条件下材料性能的变化，所以可以得到更为合理的寿命预测数据。
零部件发生疲劳失效，基本上是局部应力集中处进入塑性应变阶段，导致疲劳失效。-N法是广泛用于汽车结构件疲劳寿命计算方法，它能有效地计入缺口、焊缝、应力集中等现象所产生的局部循环塑性变形效应，该效应是材料的弹性变形和塑性变形的叠加，其数学表达式为
3.4.3 材料疲劳参数的确定
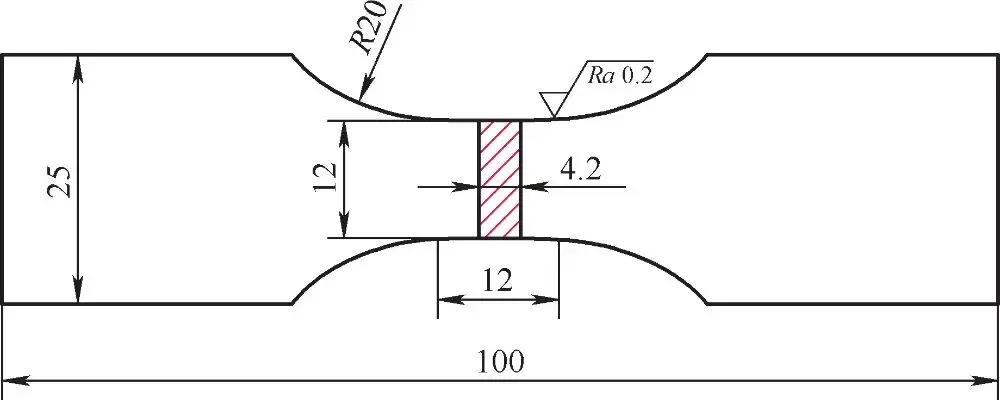
图 3-32疲劳试验试样尺寸
以 B510L材料为例， 弹性模量的测定值约为 1.99×105。试验中采用轴向应变控制，循环应变比 R1，频率为 0.1~1.0Hz（大应变时采用较低的频率，小应变时采用较高的频率），疲劳试验加载波形为三角波，试验设备为 MTS320（±250kN）电液伺服疲劳试验系统，如图 3-33所示，并采用 10mm轴向引伸计测量控制应变。试样失效确定采用载荷下降法，取峰值载荷下降到 50% 或样品断裂作为试样失效判据，定义为 Nf，并取 1/2疲劳寿命的滞后回线为稳定迟滞后回线。试验过程中记录B510L材料的总应变幅，失效循环次数与循环应力幅，具体试验结果见表 3-10。弹性应变幅值可以通过式（3-35）中弹性变形部分表达式计算，塑性应变幅值即总应变减轻弹性应变。由表3-10试验数据，绘制 B510L材料的应变 - 寿命曲线如图3-34所示。
图 3-33 MTS320（±250kN）电液伺服疲劳试验系统
表 3-10材料 B510L试验结果
其中循环应力- 应变关系式为
根据应变疲劳试验数据及式（3-38）、式（3-39）取对数后进行拟合，回归处理得到的其余应变疲劳参数。采用同样的试验方法得到车架各材料的疲劳参数见表 3-11。将表中的相关参数输入代入式（3-36）中，可得材料的应变疲劳曲线如图 3-35~图 3-38所示。
表 3-11车架各材料疲劳参数
图 3-35QSTE460的ε- N曲线
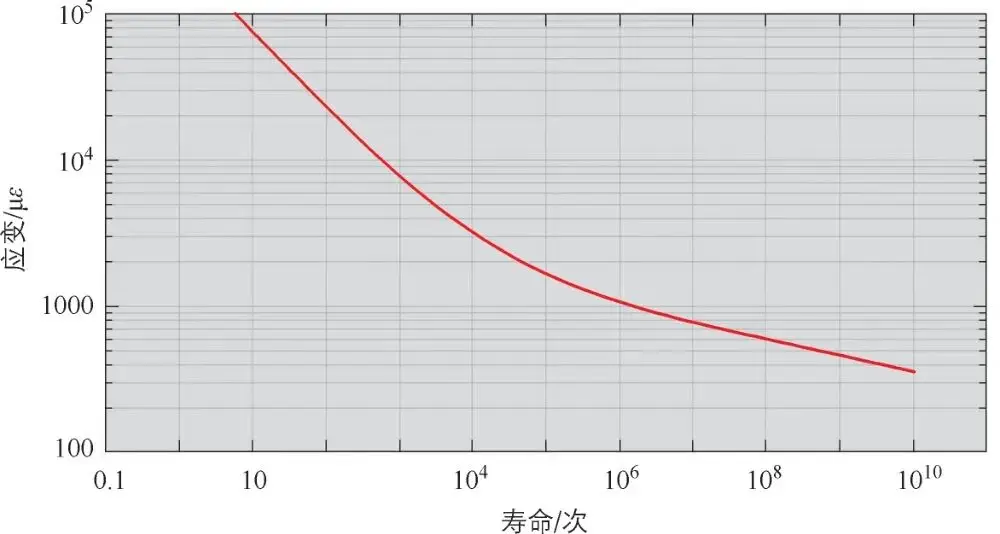
图 3-36B420L的ε- N曲线
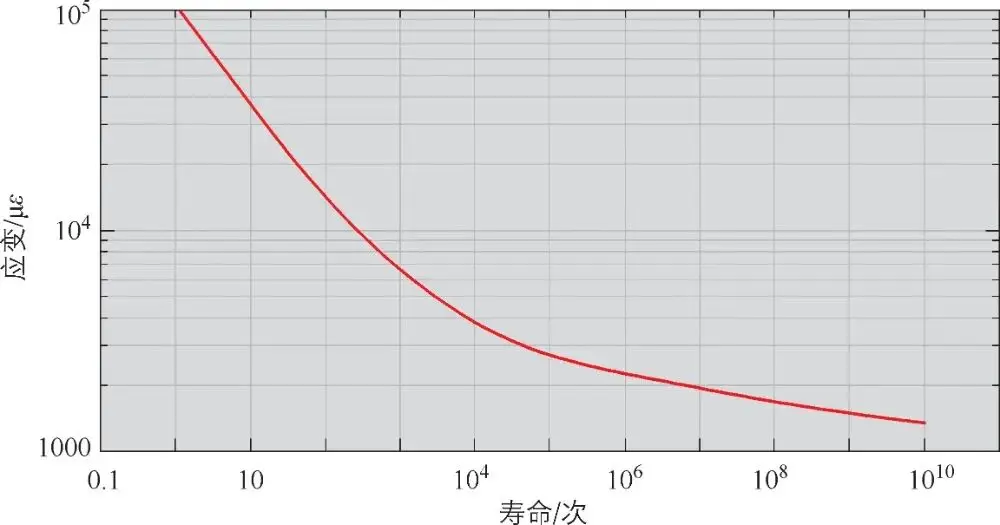
图 3-37B510L的ε- N曲线
图3-39 电动汽车车架基于道路谱疲劳载荷分解的技术路线图
（2）关键零部件的标定
本节涉及的耐久载荷分解方法，需要以关键部件路面载荷作为后续虚拟迭代工作的目标信号，实车在道路行驶过程中，弹簧、减振器、横拉杆等各零部件安装点的受力情况无法通过设备直接测量。标定技术根据力与应变之间存在的线性关系，可以很好地将零部件的应变信号转化为零部件安装点位置的力信号，通过采集零部件在不同路面产生的应变信号，并根据标定得到的力与应变之间的关系，从而转化得到安装点位置的力变化信号。所以标定结果的好坏直接影响到虚拟迭代过程载荷分解的准确性。
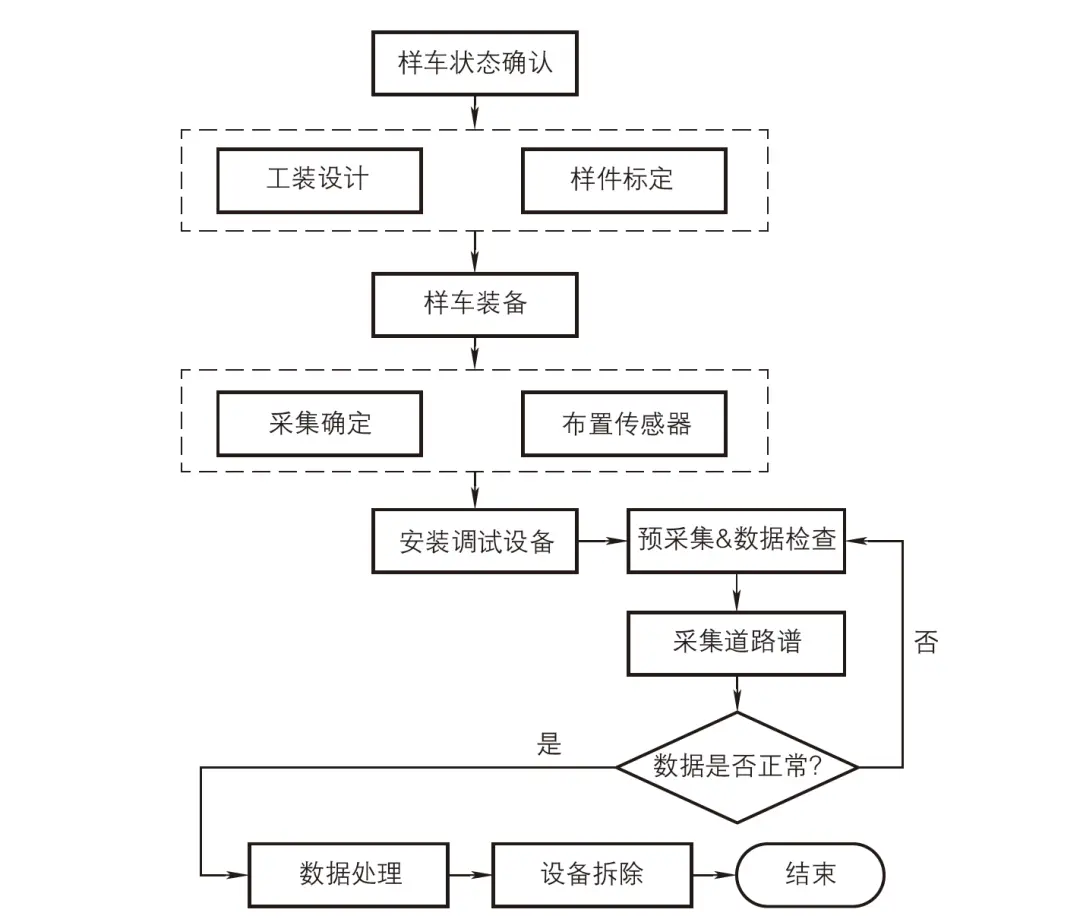图 3-40整车道路谱数据采集流程
应变的获得通常使用金属应变片进行测量。应变片是变阻式传感器的一种，其感应的基本原理是当应变片受到机械应力作用时，其电阻值会随器件的应变成比例变化。由于金属应变片的电阻变化与其应变之间存在近似的线性关系，因此测量时将应变片贴于被测物体上，当被测物体压缩和拉伸时，应变片将产生与贴片区域相同的变形，从而引起电阻的变化，进而获得被测物体的应变值。
1）减振器光杆的标定。减振器光杆标定采用 BF350-3EB型、带温度补偿的全桥应变片，应变片实物图及贴片位置如图 3-41所示。全桥电路由两个泊松应变片组成，该桥路测量拉压载荷，对弯曲、扭转和温度进行补偿，采集信号包括减振器应变信号、作动缸的加载力及位移 信号。
图 3-41应变片及其在减振器光杆上的贴片位置示意图
减振器标定过程中，减振器下端固定在台架上，与台架垂直安装，作动缸在减振器上端加载力，要求作动缸及减振器轴线在同一垂直线加载，加载力从 500~2000N加载 3个循环，减振器安装与加载如图 3-42所示。通过记录减振器的加载力与应变信号，将二者进行拟合，其拟合后的结果如图 3-43所示。
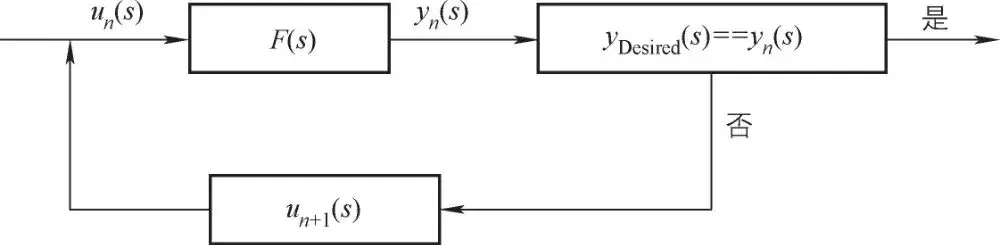图3-42 减振器安装与加载示意图
图3-43加载力与应变拟合曲线
由图 3-43可知，加载力与应变的关系式为
式中，y表示作用缸加载的力，即减振器受到的力，单位为 N。x表示减振器应变，可得标定系数为 30.177，线性拟合度接近 99.4%，线性拟合度较好。线性拟合度越接近 100%，说明线性拟合度越好，标定系数越准确。如果线性拟合度差，则考虑并检查夹具是否松动。应变片是否黏紧、应变片与信号线焊接是否良好等因素。
2）螺旋弹簧的标定。螺旋弹簧标定采用 BHF350-3HA型半桥应变片，应变片安装在螺旋弹簧中间，需考虑实车位置便于安装及检查，尽量保证左右螺旋弹簧安装位置一致，减少标定结果差异。应变片贴片位置如图 3-44所示。该桥路测量扭转载荷，对拉压、弯曲和温度进行补偿。螺旋弹簧的加载如图 3-45所示，下端固定，上端通过作动缸加载力，要求螺旋弹簧与作动缸轴线在同一垂直线上，作动缸以 7400~19000N的循环力加载 3个循环。
图3-44 弹簧应变片贴片位置示意图
图3-45螺旋弹簧加载示意图
通过采集作动缸的作用位移、作用力以及螺旋弹簧的应变 3个信号，对螺旋弹簧进行标定。加载力与螺旋弹簧应变以及作用位移与螺旋弹簧应变，拟合后的结果如图 3-46、图 3-47所示。
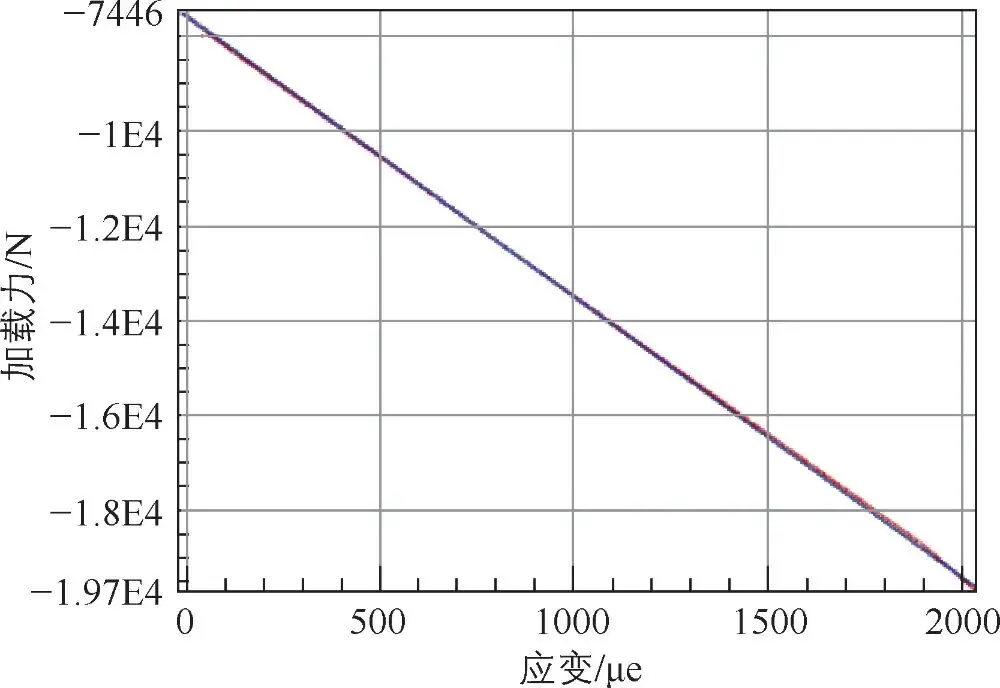图3-46 加载力与应变拟合曲线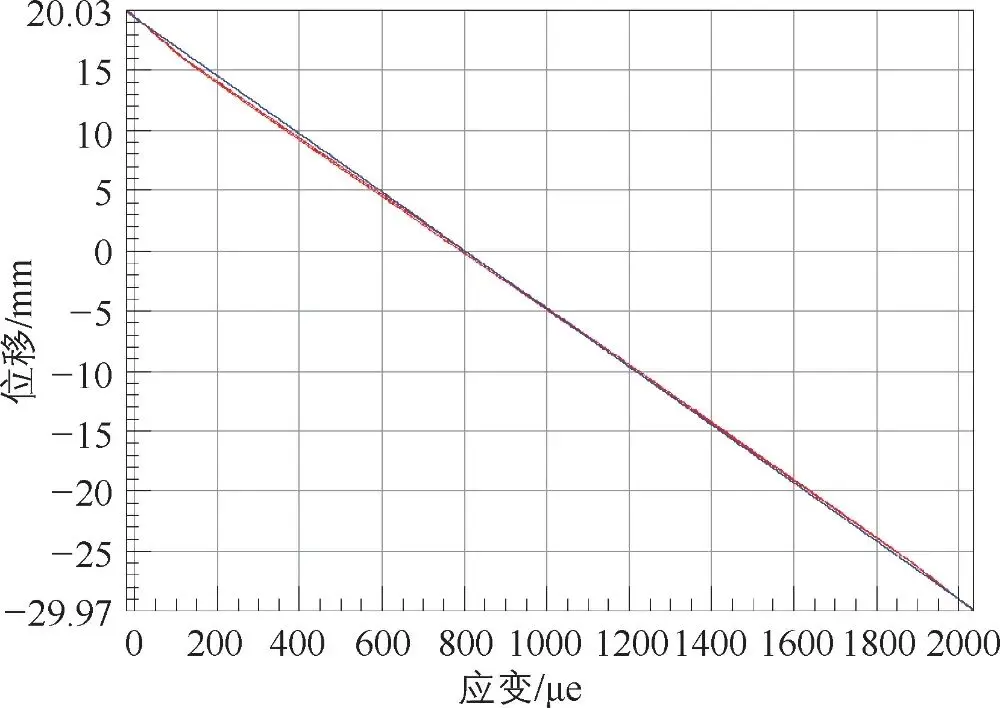
图3-47位移与应变拟合曲线
由图 3-46可知，加载力与应变的关系式为
式中，y为作动缸加载的力，即弹簧受到的力，单位为 N；x为螺旋弹簧应变，可得标定系数为
-5.921。线性拟合度为 99.9%，线性拟合度较好，标定系数准确。
由图 3-47螺旋弹簧应变与位移拟合曲线，可知位移与应变的关系式为
式中，L为作动缸加载的位移，即弹簧变形量，单位为 mm；x为螺旋弹簧应变，可得标定系数为 -0.02419。线性拟合度为 99.9%，线性拟合度较好，标定系数准确。
（3）道路谱采集的前期准备
为了获取用于多体动力学道路谱载荷虚拟迭代仿真数据，需要通过采集设备采集道路耐久试验整车的参数，采集设备的选取及采集设备的安装与布置，对后期采集数据结果能否准确反映实车状态非常关键。
1）采集设备与安装布置。采集设备是获取样车各性能参数的必备工具，为了实现道路谱载荷数据的采集，企业所提供的主要设备有：LMSSCADAS317S数据采集器、CT1010SLFP三轴加速度传感器、Kistler-S625六分力传感器等，设备实物图如图 3-48所示。
图 3-48道路谱采集设备实物图
六分力传感器负责采集在道路耐久试验过程中轮心 6个方向的载荷信号。六分力传感器的安装，由企业提供专门制作的转接件同车轮轮辋进行固定连接，如图 3-49所示。
悬架的实际位移变化数据，本书采用深圳市米朗科技有限公司生产的 WEP-M-R型拉线位移传感器进行采集，位移传感器安装在车身端，应避免与其他零部件干涉，后悬架左右两边位移传感器的安装如图 3-50所示，通过测量减振器的位移行程来代替悬架的位移行程。
图 3-50后悬架拉线位移传感器的安装
加速度传感器通常被用来获取零部件特定位置加速度数据，本书采用三轴加速度传感器进行数据采集。图 3-51所示为测量轮胎转向节位置加速度信号的加速度传感器安装示意图。
图 3-51加速度传感器安装
通过 WZX-I型转向盘力矩及角度传感器测量转向盘在试验路面过程中转向盘力矩及角度数据，以准确获取实车在测试路面的转向信息。其传感器安装如图 3-52所示。
2）采集通道的确定。根据以上试验内容的介绍，通道信号主要来自六分力仪及各类加速度传感器、拉线传感器及应变片信号等。采集通道的多少，根据车辆类型及需求确定。道路载荷谱采集通道具体信号及其通道内容见表 3-12。
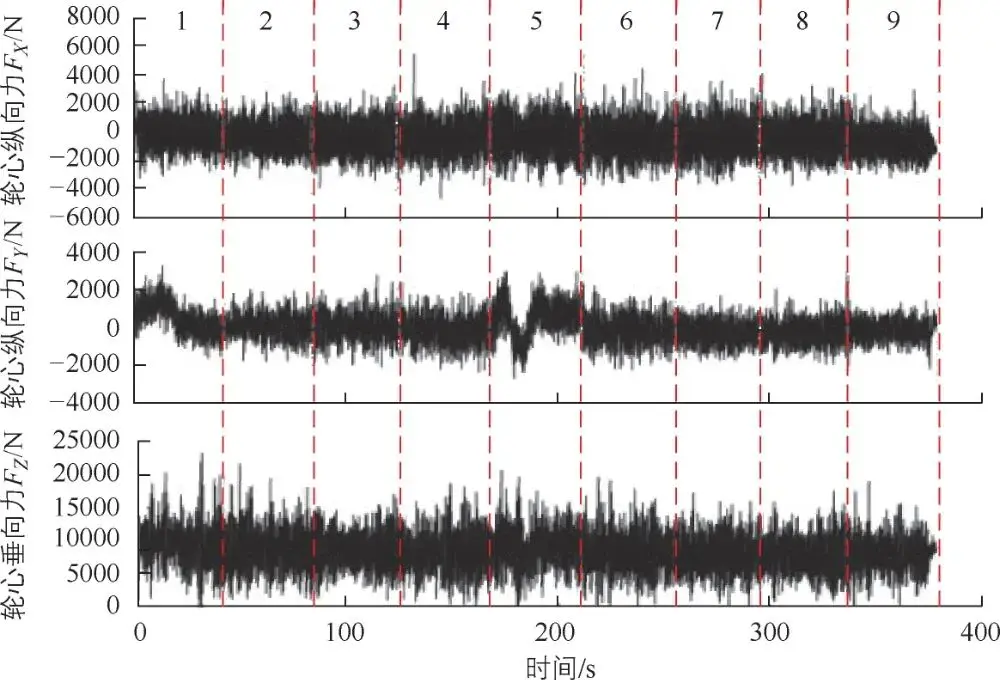
图 3-52转向盘力矩及角度传感器的布置
表 3-12道路载荷谱采集通道列表
（4）道路谱数据的采集
在完成零部件的标定及数据采集设备的安装，并确认采集样车状态可以进行采集工作后，进行实车的道路谱数据采集。在准备采集之前，需要对样车进行加载（加载到耐久实验规范载荷）及称重。同时，测试样车需记录加载前后限位块间隙、弹簧安装长度等相关参数。
图 3-53整车道路耐久试验路面采集顺序
图 3-54是根据整车道路耐久试验规范采集的基础车在强化路面中左前轮心六分力的时域载荷数据。针对采集到的数据，将通过缩减后用于虚拟迭代工作。其他通道的时域载荷数据由于篇幅有限，本书不再一一展示。
图 3-54左前轮心六分力的时域载荷数据
3.4.5 疲劳载荷循环次数的确定
由于载荷采集的道路路面比较长，如果通过虚拟迭代对所有实际路面载荷开展迭代计算，将非常耗时。因此，应在保证不影响结构件损伤的同时，对采集的道路谱数据进行处理，缩短载荷虚拟迭代的时间。通常采用的缩减技术有里程缩减、道路缩减及重量缩减，这几种缩减方法都基于伪损伤值相等的原理进行 [141]。本书主要基于里程缩减技术进行道路谱载荷的缩减，从而获得新的道路谱载荷的循环次数，用于电动汽车车架疲劳性能的分析。
道路谱载荷缩减的流程由道路谱载荷的截取、损伤值的比较、截取片段的选择、道路谱载荷缩减及结果评价等步骤组成，如图 3-55所示。道路谱载荷通常截取一些伪损伤值较高的载荷片段，然后对选择的截取片段的缩减结果进行评价，如果效果不佳，则重新选择截取片段，最终得到各片段的循环次数。
图 3-55道路谱载荷缩减的流程图
（1）伪损伤理论
在工程应用中，如分析汽车底盘及车身部件在坏路路面激励下的响应特征时，需要采集很多通道的道路载荷谱数据。这些数据均为时域曲线，通过这些时域曲线无法直接描述载荷的相对强弱关系，因此需要用一个简单的数值来描述载荷谱的严重程度。如果不考虑具体的结构，直接把各种时域信号，如力、位移、加速度、应变等看作广义应力，使用特定的标准 S-N曲线，再按照计算真实疲劳损伤相同的方式进行损伤累积计算，这样得到的损伤值叫作伪损伤（PseudoDamage）。伪损伤很好地反映了信号本身的特性，非常适用于耐久载荷的对比和等效关联，在整车及零部件耐久分析中得到了广泛应用。计算伪损伤值所用的 S-N曲线不是某种材料的实际曲线，而是一种简化的标准曲线，通常采用在双对数坐标系下进行表示。伪损伤以 S-N曲线、线性累加损伤准则和雨流计数原理为基础，首先将时域曲线通过雨流计数换算成雨流矩阵，然后根据伪损伤 S-N曲线计算时域载荷谱的伪损伤值，如图 3-56所示。后续的道路缩减处理均是基于伪损伤来进行的。
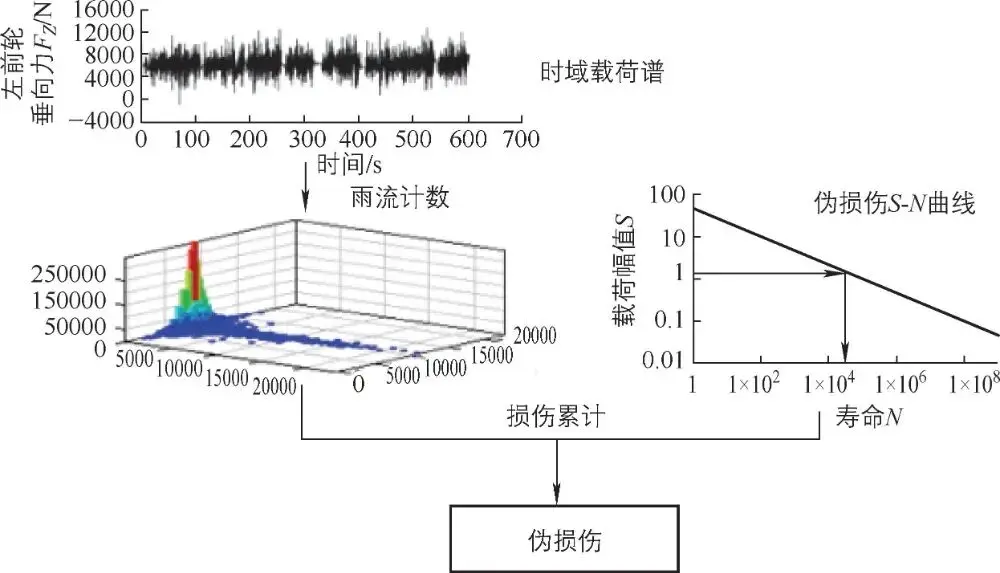
图 3-56伪损伤计算流程
不同的时域信号根据同一标准的 S-N曲线进行计算得到伪损伤值，将不规则的时域信号转换成一个固定值，可以进行方便的对比分析。如图 3-57所示，时域信号 1与时域信号 2根据同一标准 S-N曲线计算得到的伪损伤值分别为 D1和 D2。
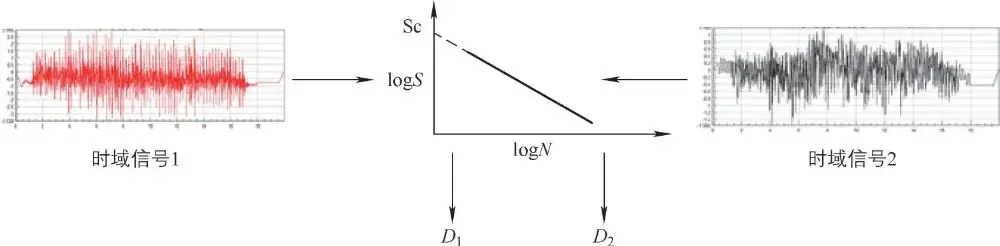
图 3-57根据同一标准S-N曲线计算伪损伤值
在同一标准下计算得到的伪损伤值，以其中一个信号伪损伤值为基准，其他信号伪损伤值与基准的比值，称为相对损伤值，见式（3-43）。
式中，R为相对损伤值。相对损伤越接近 1.0，表示对比信号之间的强度越接近。
（2）道路谱载荷的截取
如图 3-58所示，为采集比利时路的基础车轮心处道路谱载荷数据。路面总里程为 2.61km，总时长为 387s。依据均分的原则，将该道路谱载荷数据分成 9等份，即每等份时长为 43s。后续将选择这 9个载荷片段，采用等损伤原理对其进行缩减，获取尽可能少的载荷片段进行后续的虚拟迭代工作，以达到里程缩减的目的，并提高动态仿真计算的效率。
图 3-58比利时路载荷数据截取
（3）各载荷片段循环次数计算
对各片段组的优化主要依据式（3-44）及式（3-45）来进行，Target为比利时路总伪损伤矩阵，每一行代表每一个通道的伪损伤值，总伪损伤值是由企业道路耐久试验规范中比利时路的总循环次数 648次乘以采集到的单次路谱载荷伪损伤值得到的。以 Section为分割后的比利时路各载荷片段伪损伤值矩阵，每一列代表每一个片段各通道的伪损伤值，最终求解得到各载荷片段的总循环次数矩阵。
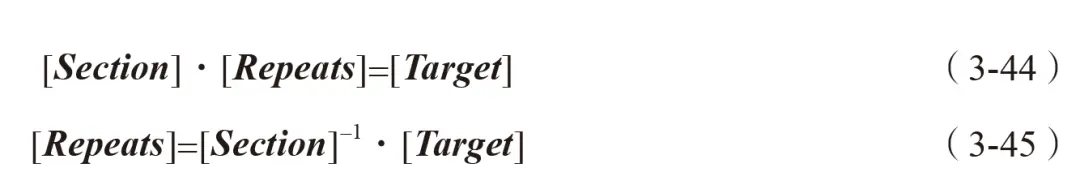
式中，Section为分割后的比利时路各片段伪损伤值矩阵；Repeats为需要求解的比利时路各片段的循环次数。若循环次数为零，则表示该路面片段被缩减掉。根据式（3-44）及式（3-45），经过组合优化，最终求解得到各片段的循环次数矩阵。
使用最佳拟合方法（BestFitOptimization，BFO）对各片段进行组合优化，目标函数为缩减后各通道损伤值与目标值之间误差 E的二次方的最小值，约束条件为每个片段循环次数≥ 0， 其表达式为
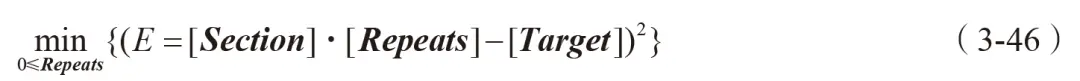
通过修改约束变量的最大值和最小值，以达到对载荷谱进行缩减的目的，优化及计算过程在 nCode软件中完成。缩减后比利时路满载各路面的循环次数见表 3-13。9条比利时路载荷片段经缩减后最终保留了 2段，即片段 2及片段 6。根据各片段总循环次数及比利时路面的实际长度，计算可得缩减前后比利时路面单次循环里程由 2.61km缩减至 0.62km，有效地缩短了路面里程。
表 3-13缩减后比利时路满载各路面的循环次数
（4）缩减前后对比分析
对道路谱各通道数据缩减前后，原始谱与加速谱吻合程度的对比判断，主要从时域、幅值域及频率域 3个方面进行分析比较。由于采用里程缩减，因此不作时域的对比，对缩减结果的评价主要从幅值域及频率域进行缩减前后对比。
针对幅值域对比，主要从雨流计数和穿级计数两个方面进行对比分析，将缩减前后的采集数据导入软件 LMStecware中进行数据处理。其中左前轮轮心垂向力缩减前后雨流计数矩阵对比如图 3-59所示，从图 3-59可以看出雨流形状的分布规律基本一致。图 3-60所示为左前轮轮心垂向力缩减前后穿级计数的对比，从图 3-60中可以看出缩减前后十分接近。
对于频率域对比，主要通过载荷的功率谱密度（PowerSpectralDensity，PSD）来进行。加速谱不仅要满足缩减前后的损伤等效，也要满足频率域上的等效。通过对比分析原始谱和加速谱前悬架左侧轴头加速度信号的 PSD来评价两种载荷谱的频率域特征是否一致，图 3-61所示为缩减前后原始谱和加速谱的 PSD分析对比，由图 3-61可以看出，加速谱和原始谱的频带为0~20Hz，在各个频率上缩减前后的 PSD分布趋势基本一致，具有相同形状的 PSD分布曲线。
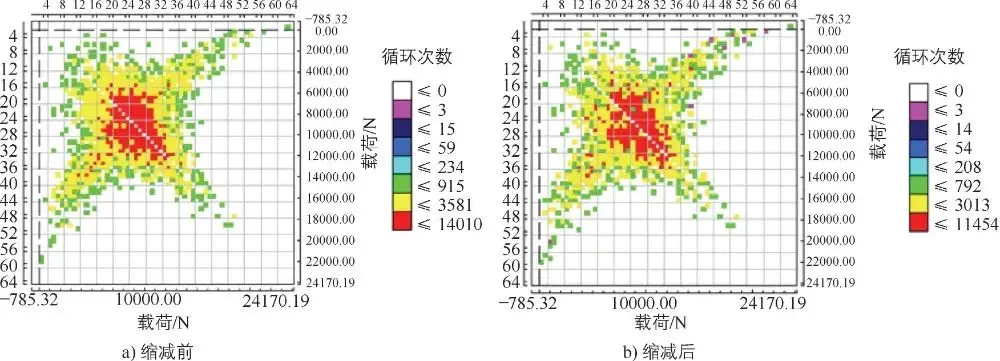
图 3-59左前轮轮心垂向力缩减前后雨流计数矩阵对比
图 3-60左前轮轮心垂向力缩减前后穿级计数对比
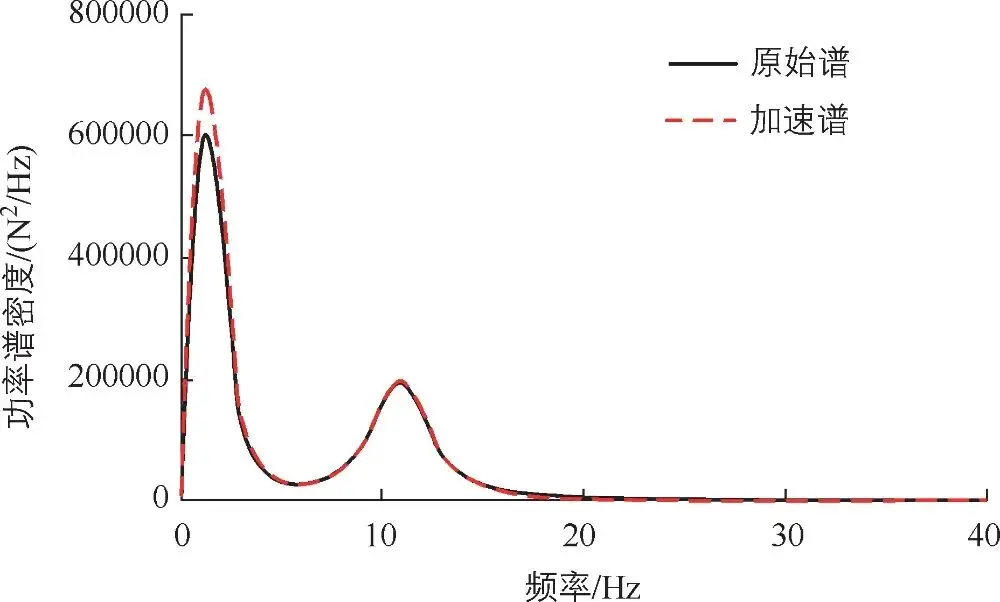
图 3-61前悬架左侧轴头垂向加速度缩减前后 PSD对比
综上所述，通过幅值域和频率域两个方面的对比，表明加速谱保留了原始谱的特征，缩减后能够实现对原始谱的替换，有利于提高车架疲劳分析效率。
根据企业的道路耐久试验规范定义的耐久循环次数，并结合对比利时路面道路缩减后的循环次数，得到用于疲劳寿命分析各路面载荷的循环次数，见表 3-14。
表 3-14用于疲劳寿命分析各路面载荷的循环次数
3.4.6 电动汽车车架疲劳载荷的获取
本节将基础车采集获得的路谱载荷数据和多体动力学仿真分析结合在一起。利用虚拟迭代的方法，获取适用于多体动力学模型的外部激励载荷。再结合多体动力学仿真分解，得到电动汽车车架的疲劳载荷。
（1）整车多体动力学模型虚拟迭代
获得零部件在车辆行驶过程中的载荷历程，是疲劳分析计算必备的前提。当前，通过多体动力学模型获取部件内部载荷为主要途径。虚拟迭代方法可以很好地获取道路谱耐久载荷 [142]。
通过上文采集的基础车轮心加速度、弹簧减振器位移、球头载荷等信号作为目标，反向推导多体动力学模型中轮心的载荷输入，用于驱动动力学模型的仿真计算。轮心驱动的反向推导，并不是对六向力进行全部推导，通常只推导出轮心垂向位移用于取代轮心垂向力，而保留其他方向上采集的载荷。通过不断的迭代推导最终获得施加在多体动力学模型轮心处的垂向位移，下文将结合这一技术原理对电动汽车车架疲劳载荷的获取展开分析。
通过激励产生的系统响应与目标信号（采集信号）的对比（相对损伤），根据其差值及系统传递函数，调整求解激励信号，直至达到理想的相对损伤，此时求解得到的激励信号即认为是接近实际采集过程中的路面激励。
根据系统激励与响应的关系，系统传递函数模型可以简化成如图 3-62所示，即给系统模型一个随机的激励信号，将会产生对应的响应信号，由此可以计算得到整车系统传递函数模型。
图 3-62系统传递函数模型
由图 3-62可知，可以得到系统的传递函数为
式中，u1(s) 为第一次计算得到的激励信号；yDesired(s) 为目标信号。根据计算得到的激励信号
u1(s) 激励系统模型，将得到响应信号与实测的目标信号进行对比。
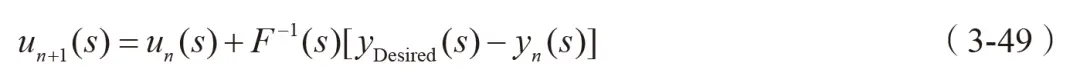
式中，un+1(s) 为第 n+1次求解得到的激励信号；yn(s) 为计算得到的第 n次响应信号。若 yn(s) 不满足要求，则重新计算激励信号 un+1(s)，以此不断进行迭代，直至满足要求为止。该虚拟迭代原理如图 3-63所示。
图 3-63虚拟迭代原理图
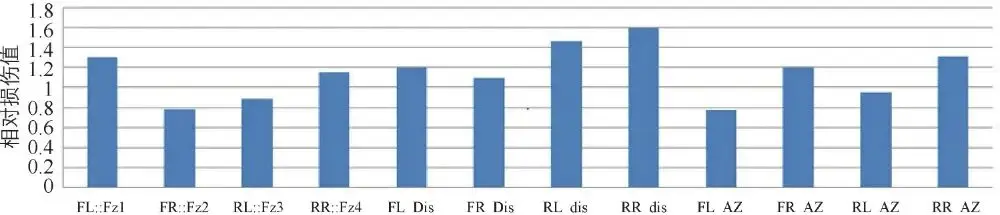
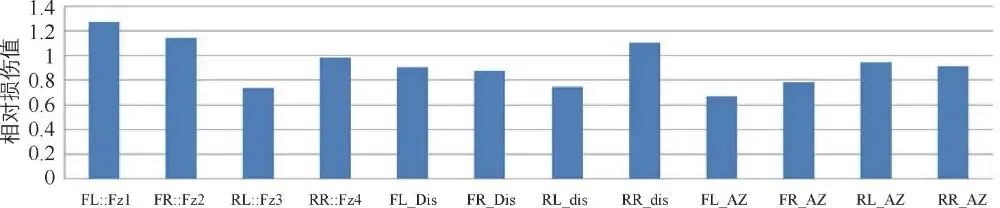
图 3-64长波路相对损伤
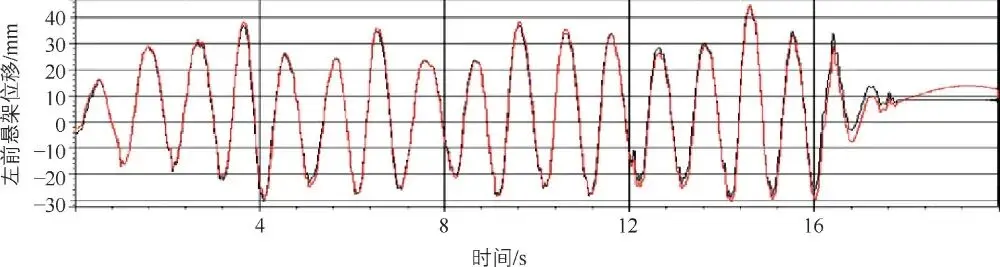
图 3-65长波路目标时域信号与迭代时域信号对比
图 3-66比利时路相对损伤
图 3-67比利时目标时域信号与迭代时域信号对比
从图 3-64~图 3-67的迭代结果可以看出，各路面相对损伤值均在 0.5~2之间，迭代信号与目标信号在时域吻合度高，迭代结果比较准确。迭代获取的路面不平度可以作为电动汽车疲劳载荷分解动力学模型的输入激励。
（2）电动汽车车架疲劳载荷的分解
通过虚拟迭代计算可以得到基础车各路面不平度结果，在保证电动汽车底盘外连点及底盘性能参数与基础车相同的情况下，可以将基础车迭代得 到的垂向路面不平度激励加载到电动汽车多体动力学模型上 [149]。由于基础车与电动汽车的轴荷不同，即使在相同的路面下，除垂向位移载荷外，基础车采集的其他方向的轮心力不能直接作用于电动汽车多体动力学模型上。但两者的轮心在其他方向的力存在线性关系，这种关系表现为两款车的轴荷之比，见式（3-50）。因此，可以对基础车采集的轮心五分力信号进行缩放（系数），从而实现轴荷转移，作为电动汽车的激励信号。利用这种关系，可以在电动汽车样车还没试制出来之前，提前预测电动汽车的疲劳性能，以提高产品研发效率，缩短研发周期。这种方法也称之为轴荷转移法。由于电动汽车车架外连点及底盘性能参数与基础车相同，因此，可以通过这种方法得到电动汽车车架疲劳载荷，用于分析及优化电动汽车车架耐久性能。
通过虚拟迭代得到的基础车路面激励作为电动汽车轮心的 Z向激励，电动汽车轮心其他方向的五分力可以运用基础车采集的六分力数据（Z向力除外），将轮心五分力乘以轴荷转移系数，轴荷转移系数见表 3-15，即可得到用于驱动电动汽车多体动力学模型中轮心的五分力。
用基础车迭代得到的各路面激励信号及通过轴荷转移系数得到的轮心五分力信号激励电动汽车多体动力学模型，基于多体动力学理论，在 ADAMS中进行仿真计算。其中，载荷分解提取得到的电动汽车车架钢板弹簧前卷耳位置的搓板路路谱疲劳载荷如图 3-68所示，该载荷包含
了车架钢板弹簧前卷耳位置处 6个方向的时域载荷。同理，获得车架不同外联点位置在其他路面行驶中的载荷，以 rsp文件的形式可直接作为电动汽车车架疲劳性能分析的载荷输入。
表 3-15轴荷转移系数
图 3-68车架钢板弹簧前卷耳位置搓板路路谱疲劳载荷
3.4.7 电动汽车车架疲劳性能的分析
由于获得的路谱疲劳载荷属于时域载荷，因此对车架进行疲劳分析时，首先需要获取其在单位载荷作用下的应力分布。于是，基于电动汽车车架有限元模型对其各个外连接点施加单位载荷，即 X、Y和 Z方向分别加载单位载荷（1N和 1N·mm），基于 Nastran求解器并且采用惯性释放方法对其进行计算，得到车架在单位载荷作用下的应力应变分布结果。图 3-69所示为左前减振器支架在 X方向加载 1N时的应力分布云图。由图 3-69可知，左前减振器支架在单位载荷作用下的最大应力为 0.05MPa。图 3-70所示为左下摆臂前支架在 X方向加载 1N·mm时的应力分布云图。由图 3-70 可知，左下摆臂前支架在单位载荷作用下的最大应力为 3.66×104MPa。以此类推，可以获得每个外连点 6个方向上的单位载荷应力分布。
因此，基于上文中获得的各个路面的路谱疲劳载荷和定义的各个路面对应的循环次数，再结合试验获得的材料曲线和应变- 疲劳曲线，采用 Neuber修正法，通过疲劳累积损伤理论，在Ncode软件中进行计算，可以实现对电动汽车车架疲劳损伤的预测分析。
如图 3-71所示，为电动汽车车架路谱疲劳损伤分布图。由图 3-71可知，该电动汽车车架路谱疲劳的最大损伤值为 0.42，位于货厢后左安装支架处，其第四横梁与纵梁连接处的损伤值为 0.2，前电池包后安装支架的损伤值为 0.177，前悬架右上跳限位块安装支架的损伤值为0.073，其他部位区域为无限寿命，车架整体的损伤值均低于实际工程要求值（1.0）。
图 3-69左前减振器支架在X方向加载 1N时的应力分布云图
图 3-70左下摆臂前支架在X方向加载 1N·mm时的应力分布云图
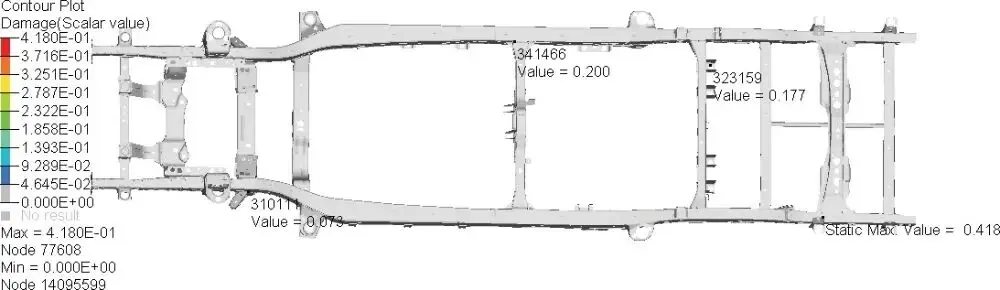
图 3-71电动汽车车架路谱疲劳损伤分布图
因此，该电动汽车车架能够满足疲劳设计要求，具有较高的疲劳安全系数，发生道路耐久失效风险概率较低，其疲劳性能满足实际工程应用要求，并且具有一定的疲劳安全余量和优化空间。
本章利用有限元求解软件 Nastran，对电动汽车车架有限元模型进行了模态性能和刚度性能分析。重点结合力学理论推导和多体动力学模型对电动汽车车架的强度载荷获取展开了研究，基于车架强度载荷和强度分析方法完成了车架多工况强度性能的仿真分析。同时，对电动汽车车架疲劳载荷的获取以及疲劳载荷循环次数的确定进行了分析，并根据疲劳分析理论及方法，实现了对电动汽车车架疲劳性能的预测分析。通过研究车架性能指标对电动汽车车架开发的影响，发现电动汽车车架模型基本能满足模态、刚度以及疲劳性能的要求，但电动汽车车架的强度性能，在较为严苛的制动工况和转弯制动工况中会存在一定的失效风险，需在后续的优化工作中解决这一问题。
内容简介：本书以新能源汽车产业发展状况为背景，总结新能源汽车开发过程中存在的问题，并以车架结构性能为分析目标，层层递进引入研究相关的理论基础、技术方案、设计方法及其发展趋势。具体来说，本书根据产品开发流程介绍了新能源汽车的发展背景、相关的软件、硬件及算法基础。在此基础上，本书沿着新能源汽车开发的技术路线，结合多体动力学与有限元法，重点介绍了车架的载荷获取方法以及结构性能分析方法，并基于车架结构性能的分析，对车架多性能匹配的优化策略进行研究，建立了适用于电动汽车车架的多目标优化方法及流程，为电动汽车车架的开发提供技术支持和理论依据。另外，本书还介绍了上述开发及测试所用的工具及操作流程，帮助读者进行实践。最后，本书展望了新能源汽车技术未来的发展趋势以及需要解决的问题。
本书适用于对新能源汽车结构设计及优化技术感兴趣的读者，包括开发人员、设计人员、科研工作者等。本书还适用于有相关知识背景的从业人员。
作者简介
余祯琦：博士、高级工程师、九三学社社员。以第一作者发表SCI论文1篇，EI论文3篇，以第一发明人授权发明专利2项，参与完成国家自然科学基金1项，参与完成多项企业乘、商用车型开发，获得中国数字仿真科技卓越应用奖1项、企业科技进步二等奖2项、三等奖1项、科技创新大赛优胜奖1项、优秀创新团队称号1次。
本书由机械工业出版社出版，本文经出版方授权发布。
来源：汽车测试网
