幅频响应以双对数标尺绘制。放大(或衰减,以dB为单位)根据对数频率绘制(必要时归一化频率)。在幅频响应中,通带、阻带和过渡带(图5)有质的区别:
通带(Pass Band):通带中的数据直接传送给输出,作为输出的时间历程。为了确保通带中的数据与原始时间历程数据相同,滤波器中应该没有纹波(ripple)。纹波会导致幅值随频率的轻微变化。理想情况下,在这个频带内,滤波器的增益应为0dB(即输出=输入,不改变信号的频率成分)。
渡带(Transition Band):根据应用(阶数、算法等)的不同,在通带和阻带之间的过渡带的频率宽度应尽可能窄。算法和滤波器阶数都决定了通带和阻带之间过渡的快慢。理想情况下,过渡带内的斜率尽可能陡(大幅衰减这些频率成分的幅值),从通带到阻带的拐弯尽可能急剧变化。
阻带(Stop Band):如果阻带有波纹,阻带也可能包含数据。在某些应用中,由于波纹导致的幅值可能很小,可能无关紧要。但在其他一些应用中,阻带的波纹可能不可接受。理想情况下,阻带的增益应为负无穷大(即输出=0),能完全移除这些频率成分。
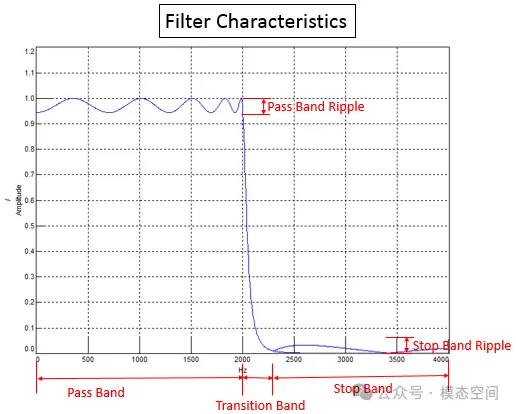
图5 以低通滤波器的幅频为例说明通带、阻带和过渡带
在过渡带,为了描述其衰减,通常按衰减量以dB/10倍频(dB/dec)或dB/倍频程(dB/otc)表示过渡带的衰减斜率。对于低通和高通滤波器,衰减量为每个滤波器阶数增加20dB/dec或6dB/oct。因此,滤波器可以用过渡带衰减量和滤波器阶数来表征。在从通带到过渡带的拐弯处,增量额外由滤波器类型决定,并且偏离渐近线。
截止频率fc是衰减3dB对应的频率。这个定义没有约束力,但是经常这样定义。在截止频率fc处,由于技术上的实现,滤波器不具有无限大的边缘陡度,约为输入信号的70%幅值在输出端仍然是可测量的(-3dB)。以低通滤波器为例,-3dB频率定义的截止频率为
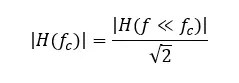
在测量应用中,这意味着描述了一个误差,这个误差在截止频率处近似为30%,是一个相当大的误差。如果我们想要估计正弦信号的均方根值(RMS),就必须仔细评估滤波器截止频率的影响。
滤波器的阶数直接决定了过渡带的衰减斜率,阶数越高,过渡带的衰减斜率越陡峭。另一方面,阶数越高,计算时间越长,导致计算效率低下,同时也使得时间延迟更长。图6显示了IIR巴特沃斯滤波器在相同截止频率、不同阶数下的过渡带衰减斜率。可以看出,滤波器阶数越高,斜率越大,阻带内的衰减越快。为了分离出频率范围,可尝试使用尽可能高阶的滤波器,但是高阶滤波器的计算效率会降低,同时,时间延迟会增加。因此,选择合适的阶数,需要在这些方面做出权衡。
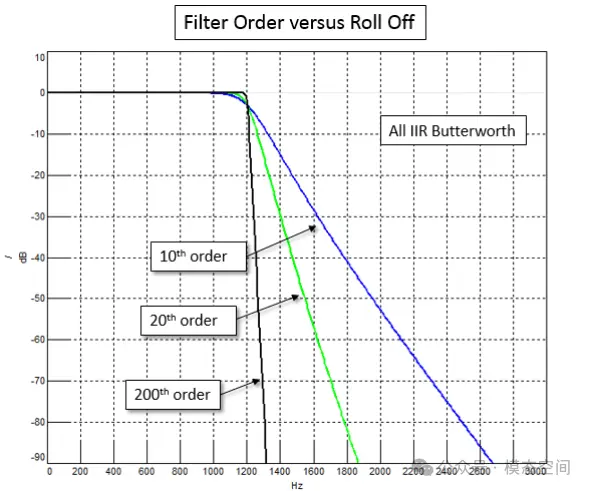
图6 不同阶数的IIR巴特沃斯滤波器的幅频响应
除了滤波器阶数外,滤波器类型也起作用。将巴特沃斯滤波器与贝塞尔滤波器和切比雪夫滤波器在4阶滤波器(斜率相同)和截止频率相同的情况下进行比较(图7)。对于阻带内的频率,贝塞尔滤波器的阻带衰减较慢,切比雪夫滤波器的阻带衰减较巴特沃斯滤波器快。然而,切比雪夫滤波器在通带中表现出纹波(特别是在截止频率区域),即输出信号在通带中也作为频率的函数被放大或衰减。
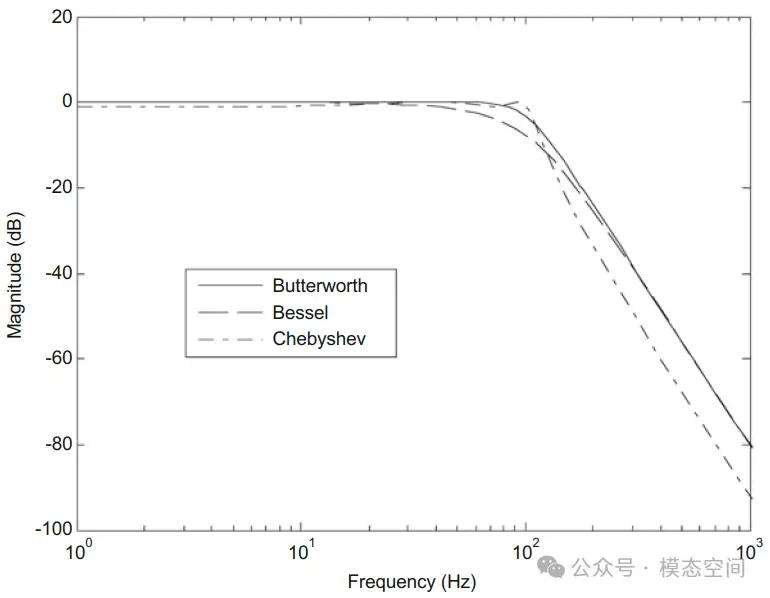
图7 4阶巴特沃斯、贝塞尔和切比雪夫滤波器的幅频响应
相频响应和群延迟
如果经滤波器输出的信号与输入之间同相位(相位差为0),那么,滤波器不存在时间延迟。但实际上,一个时域信号经滤波器后的输出,与原始时域信号相比,总存在或大或小的时间延迟,时间延迟(时移)会引起相位移动(相移),如图8所示。图中上部给出了滤波前(红色)的原始时域噪声信号(输入)和滤波后(绿色)的时域信号(输出),对比两个最大幅值位置,可以看出存在明显的时间差(时间延迟),这样滤波后的信号将不再与同步采集的振动信号在时间轴上对齐。可能在一些应用场景中,这个时间延迟无关紧要。但在另外一些应用中,这个时间延迟却至关重要,例如:
故障排查:对于多通道同步采集的噪声和振动数据,如果仅对噪声数据进行滤波,则会导致滤波后的噪声数据相对于振动数据有时间延迟(见图8)。当试图弄清楚振动事件是否产生了噪声时,这种时间延迟将使我们很难看出振动和噪声事件是否相关。
ODS分析:如果在工作变形分析(ODS)中,仅对部分振动通道应用了滤波器,而其他的没有,这将导致这些通道之间的相位关系被改变。因而,ODS动画将不正确,影响工程决策。
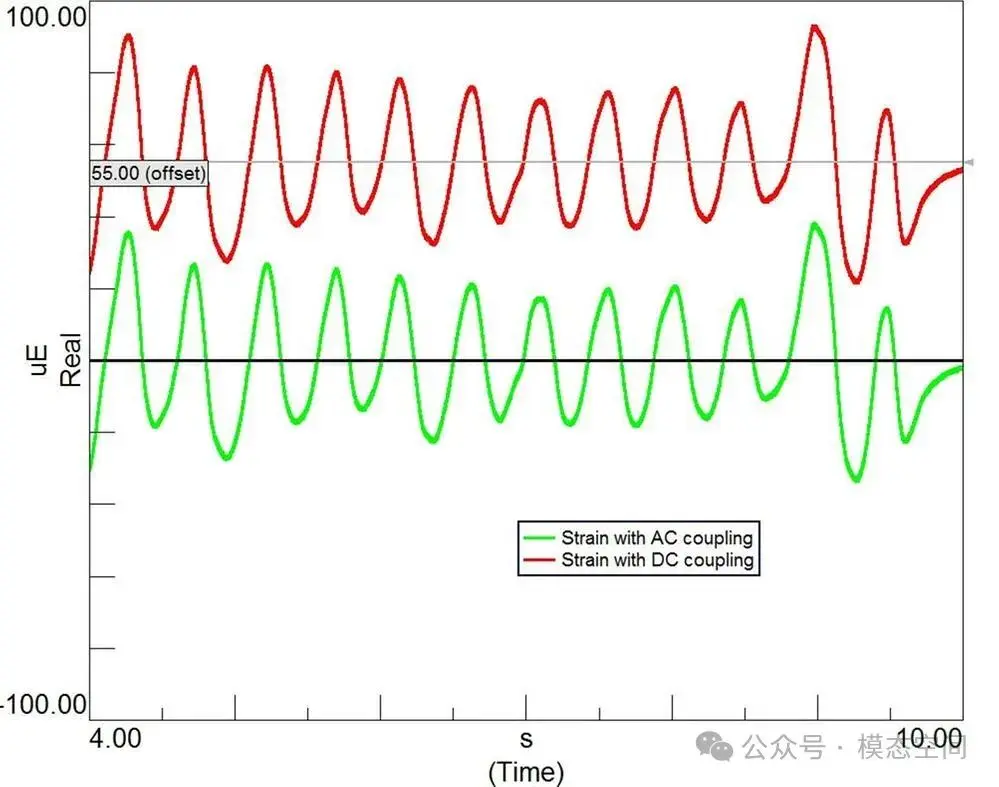
图8 滤波前后的信号存在明显的时间延迟
由于输出与输入信号之间存在相位差,因而,滤波器的相频响应也是滤波器特性之一。滤波器的相频响应描述了相位角φ的频率依赖性。在这里,相位角φ在对数频率轴f(或角频率ω)上绘制线性幅值(以度或弧度为单位)。滤波器会引起输入和输出信号之间的相位变化。以低通滤波器为例,在截止频率处相移为90°。当滤波器阶数较高时,接近截止频率时发生180°的相位跳变。相位跳变的原因是arctan函数只在-180°到+180°范围内有解。相移也发生在滤波器的阻带中。然而,由于该频率范围内的阻带衰减较大,因此该频率范围内的相移没有实际意义。
以巴特沃斯低通滤波器为例(图9a),所有三个滤波器的相频响应都显示出频率相关的相移。随着滤波器阶数的增加,越接近截止频率,相移增大。如果将不同类型的滤波器以相同的滤波器阶数与巴特沃斯滤波器进行比较,则贝塞尔滤波器的相移较小,切比雪夫滤波器的相移较大(图9b)。
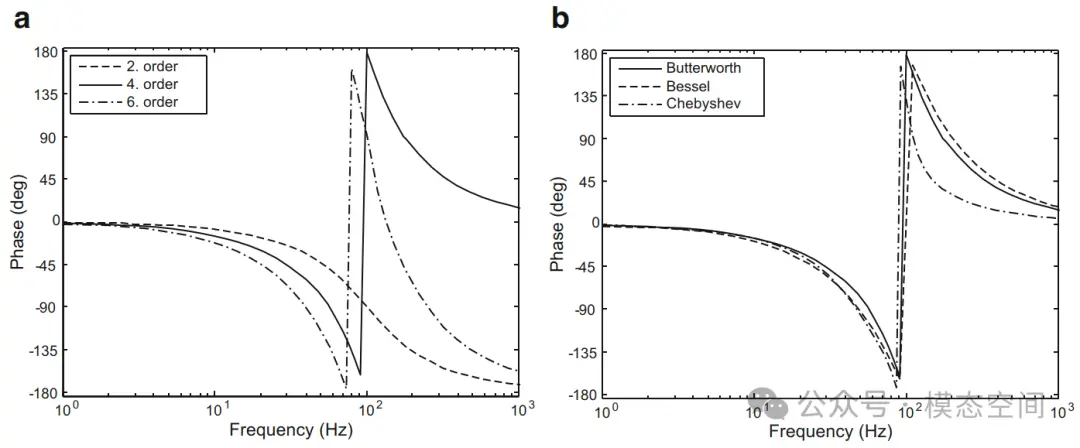
图9 2、4和6阶巴特沃斯低通滤波器的相频响应(a);比较4阶低通巴特沃斯、贝塞尔和切比雪夫滤波器的相频响应(b)
理想情况下,所有信号频率的相移量应该是相同的(FIR滤波器满足这个条件)。如果不满足这个条件,则各个信号分量根据其频率经历不同的相移,或者说相移量是频率的函数。这被描述为群延迟。相位在角频率上的负增长称为群延迟,它描述了正弦信号在滤波器中的传播时间:
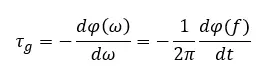
与频率无关的群延迟意味着信号在滤波器中延迟的时间相同,与频率无关。与相移相比,从群延迟中无法获得定性的描述。然而,群延迟的说明规范往往比相位角更具描述性。群延迟的频率依赖性意味着信号分量以不同的速度通过滤波器。与输入信号相比,这会导致输出信号失真。
随着滤波器阶数的增加,通带内的群延迟(图10)会变大。所考虑的巴特沃斯低通滤波器的最大群延迟发生在截止频率附近。滤波器阶数越高,最大群延迟值越明显。因此,滤波器的阶数会影响输出信号的时间延迟。所有类型的滤波器都会产生时间延迟,无论是模拟滤波器还是数字滤波器。依赖于滤波器特性,时间延迟或长或短,它们也随频率成分变化。
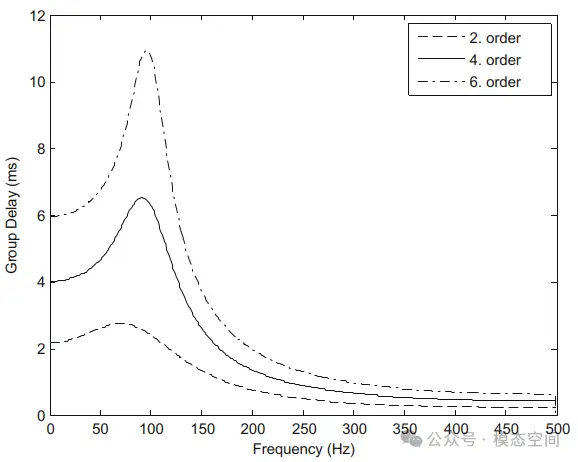
图10 2、4和6阶巴特沃斯低通滤波器的群延迟
输入信号经滤波器滤波后输出,这种方式,我们称为直接滤波。直接滤波总是会产生时间延迟,为了消除滤波器输出信号中时间延迟,可以通过时间轴向前和向后滤波数据来实现。在对输入信号滤波后,创建新的输出信号,新输出信号中的数据点按时间顺序反向再次输入数字滤波器中,消除时间延迟。这被称为零相位滤波。如图11所示,对比原始信号(红色)、直接滤波后的时域信号(绿色)和零相位滤波信号(蓝色)可以看出,零相位滤波信号与原始信号时间上是对齐的,不存在时间延迟,但直接滤波的信号存在时间延迟。但在零相位滤波信号的末端,由于没有更多的数据用于滤波,这会导致在数据末端出现数据丢失。
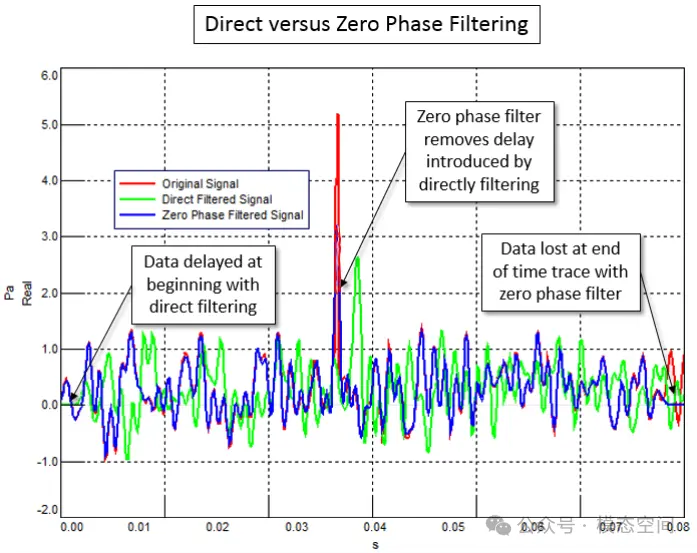
图11 对比直接滤波与零相位滤波的结果
虽然零相位滤波器的输出在时间轴上与原始输入信号对齐,但是由于数据被滤波两次,因此,衰减将加倍。故,使用零相位滤波器时有一些权衡:
计算需要两倍的时间来执行。只有数字化的数据易于实现,模拟信号难以执行。滤波后,在时域波形的末端会出现数据丢失。
来源:模态空间
作者:谭祥军












