04、滤波器的瞬态响应
传递函数描述稳态下的传递行为是所有瞬态过程衰减之后,记录时域的动态过程,例如,对阶跃函数的阶跃响应。
滤波器
输入的阶跃函数
是输入信号在t=0时从0到1的阶跃,可以可视化为方波信号的上升沿或被测信号的开启。
阶跃响应是
滤波后的信号作为系统对输入信号的响应。如果群延迟是频率相关的,则阶跃函数的信号分量以不同的速度通过滤波器。在阶跃响应中,输出端的方波边缘会出现畸变。
上升时间,瞬态时间和延迟时间
上升时间TA被理解为,滤波器对输入从0无限快速跳变到1(矩形信号的上升沿)的响应的时间跨度。上升时间有几种定义,除了拐点处的切线外,还使用10%和90%幅值对应的时间差来定义。在上升之后,可能会出现阶跃响应的过冲(overshoot),随后是衰减振荡。直到过冲消退并达到稳态终值的时间称为瞬态时间。稳定时间取决于上升时间和幅值公差带(通常定义为±5%)的定义。稳定时间是上升时间的2.2~3倍。
截止频率fc与上升时间TA的关系近似如下
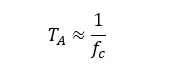
结果表明,滤波器的阶数和类型对上升时间有影响。对于AC耦合高通滤波器,如果截止频率为0.5Hz,则上升时间非常显著:上升时间为2秒。作为一个粗略的经验法则,到过冲衰减,稳定时间应该考虑3倍的上升时间。在放大器的输入电路中,AC耦合高通滤波器常用于从直流电路中分离出测量信号。然而,这种电流隔离可能导致更长的稳定时间,例如,在用一个A/D转换器采集多个模拟信号的多路复用中(早期多采用这种方式,现今普遍一个通道对应一个A/D转换器)。
2阶、4阶和6阶巴特沃斯低通滤波器对阶跃函数的响应如图12a所示。在这个例中,截止频率fc=100Hz,响应的上升时间TA=0.01s,使用3倍因子,稳定时间为0.03s。阶跃响应相对于作为输入的阶跃函数在时间轴上有移动(时间延迟)。过冲消退时间和瞬态时间随滤波器阶数的增加而增加(见图12a)。滤波器也会改变阶跃函数的幅值。阶跃函数在输入处的值是1不代表滤波器在输出端响应也为1,因为在瞬态时间内会出现过冲。随着滤波器阶数的增加,过冲的峰值也增加。必须强调一点,这些过冲是滤波器对阶跃函数的响应。相反,传输一个正弦信号,滤波器不存在过冲。
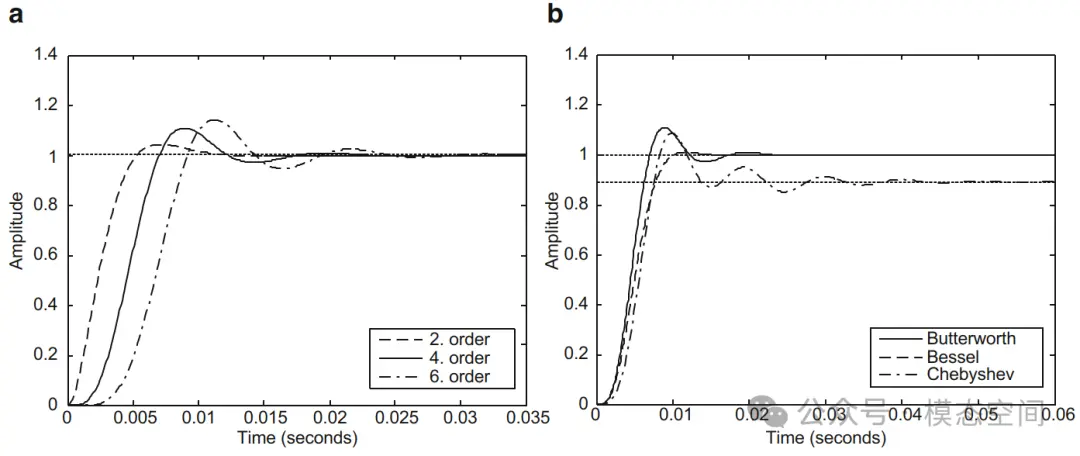
图12 2、4、6阶巴特沃斯低通滤波器的阶跃响应(a),4阶巴特沃斯、贝塞尔和切比切夫低通滤波器的阶跃响应(b)
在图12b中,对比了4阶巴特沃斯滤、贝塞尔和切比雪夫滤波器,贝塞尔滤波器的过冲最小,切比雪夫滤波器的过冲最大。切比雪夫滤波器稳态后增益幅值小于1。与巴特沃斯滤波器相比,贝塞尔滤波器的上升时间较长,切比雪夫滤波器的上升时间较短。
05
—
频带滤波器的相关定义
对于带通、带阻和陷波滤波器而言,需要定义特定的频带,允许(带通)或阻隔(带阻)或大幅衰减(陷波)这个频带内的信号,这些需要定义特定频带的滤波器统称为频带滤波器(Band Filter)。
对于频带滤波器,下截止频率fl和上截止频率fu参考滤波器的中心频率fm。绝对带宽B定义如下:
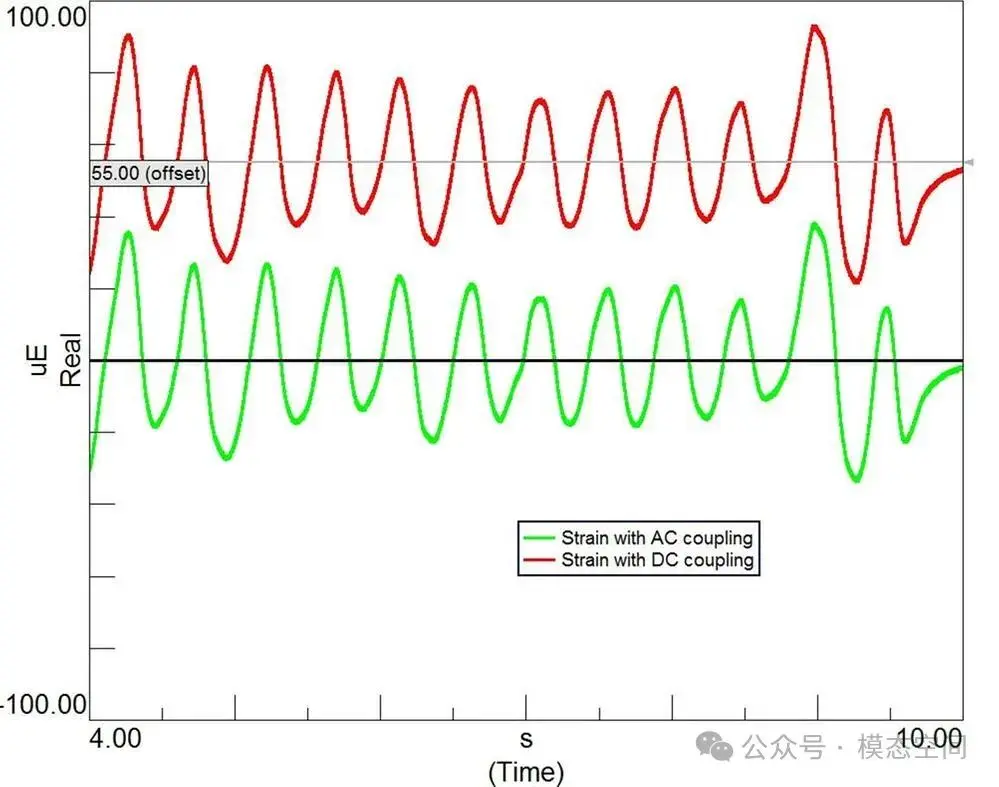
中心频率为两截止频率的均方根:
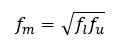
由此可以计算出相对带宽Δfrel:

滤波器品质Q定义为相对带宽Δfrel的倒数:
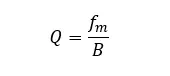
如果改变带通滤波器的中心频率,必须区分两种类型的滤波器:
恒定绝对带宽滤波器(B=常数):随着中心频率的增加,相对带宽Δfrel随1/fm减小。
恒定相对带宽滤波器(Δfrel=常数):对于这类滤波器,绝对带宽B与中心频率fm成比例增加。这类滤波器的典型例子是倍频程滤波器,其上截止频率fu和下截止频率fl的比例为2:1,而1/3倍频程滤波器是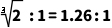 。
。
带通滤波器的上截止频率和下截止频率通常(但不是统一地)指定为3dB带宽,在该带宽处,传递幅值比中心频率处或相对于平均传递幅值小3dB。作为这种方法的替代方法,利用有效噪声带宽将滤波器与具有相同中心频率和无限陡峭边缘的理想滤波器进行了比较。对于白噪声激励(恒功率谱密度),设置上截止频率和下截止频率,使实际滤波器和理想滤波器的总传输功率一致。对于低阶的滤波器,3dB带宽和有效噪声带宽可能不同。图13显示了带通滤波器低频fl=10Hz和高频fu=1000Hz,-3dB带宽的幅频响应。传递范围内60dB/dec的斜率对应于高通和低通的3阶滤波器。

图13 带通滤波器的幅频响应
06、模拟滤波器
来源:模态空间
作者:谭祥军












