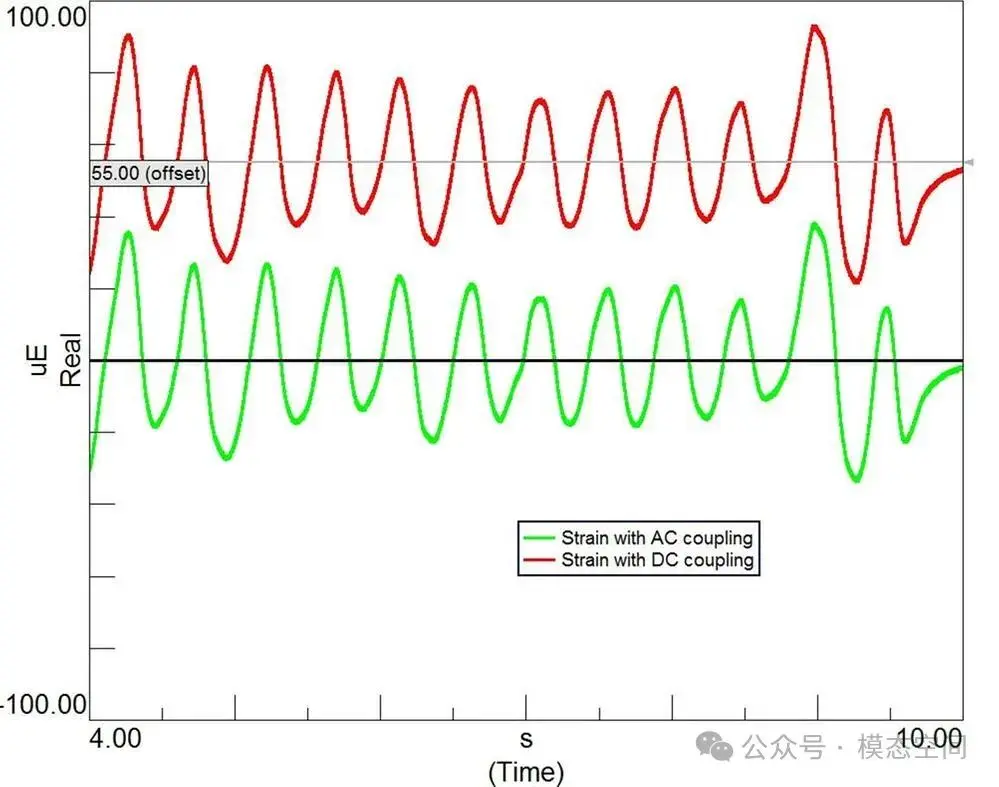
图21 AC与DC耦合的应变测量结果
因此,从图21可以看出,AC耦合会进行高通滤波。实际上,AC耦合滤波器是一个高通模拟滤波器(在ADC之前进行滤波),常见的高通滤波截止频率有0.05Hz、0.5Hz和7Hz。所有类型的ICP/IEPE型传感器或不关心直流偏置时,都应使用AC耦合方式。
图22给出了AC耦合滤波器的滤波特征(高通截止频率0.5Hz)。滤波器的高通截止频率是在信号幅值的0.707倍处,也就是-3dB幅值处。当然这个截止频率是耦合电路的函数,依赖于你使用的电子元器件。因此,AC耦合会移除信号中的直流分量,但同时也会衰减额外的低频段,如图中的0~0.5Hz。
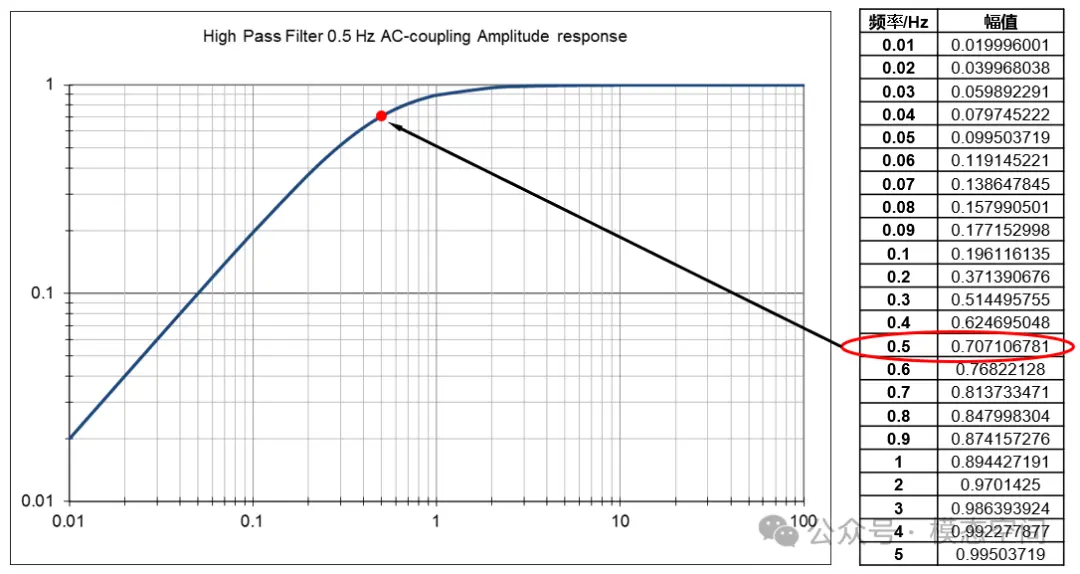
图22 AC耦合滤波器特性(高通0.5Hz)
倍频程滤波器
在声学领域中,通过设置一组平行带通滤波器来分析信号的频率成分是非常常见的,这些平行带通滤波器的时域输出信号可进行多种分析,如实时倍频程谱分析(图23)。滤波器的带宽通常为1个倍频程(1/1倍频程)或有时为三分之一个倍频程(1/3倍频程),中心频率和滤波器特性在欧标IEC 61260(1995)、美标ANSI S1.11(2004)和国标GBT 3241(2010)中均进行了标准化定义。这些标准是兼容的,因此,中心频率和滤波器形状是相同的。关于1/n(n=1,3,6,12,24)倍频程的定义及相关介绍可参考之前的文章“什么是倍频程”。

图23 倍频程滤波器工作过程示意
倍频程滤波器是频带滤波器,随着中心频率的增加,其倍频程带宽越宽,因此,通常倍频程滤波器采用恒定相对带宽方式,这样带宽正比例于中心频率。对于实时倍频程滤波而言,还有一个重要的参数是时间常数。时间常数描述的是当输入信号变化时,输出信号能变化多快。当测量的信号是非稳态信号时,带通滤波的信号的有效值将随时间变化。对于带通滤波器而言,时间常数通常近似是频带的倒数。对于恒定相对带宽的倍频程或1/3倍频程滤波器而言,不同频带具有不同的时间常数,越低频,时间常数越长。
这些倍频程滤波器的增益被允许在确定的范围内变化,并且根据标准中定义的级别(1级,2级)不同,滤波器的增益边界范围不同,如图24所示是中心频率为1000Hz的1/3倍频程带通滤波器的实例。你可以自己定义与上述标准一致的数字滤波器。但是,必须对滤波器形状进行检查,因为中心频率与采样频率的比值达到一定时,将不满足标准规定的边界限制条件。
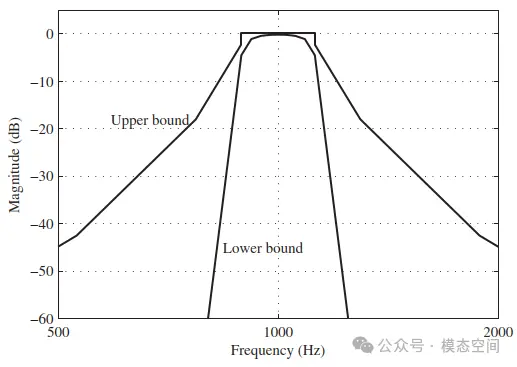
图24 中心频率为1000Hz的1/3倍频程滤波器实例
频率计权滤波器
许多振动噪声应用包括某种形式的频率加权,如IEC 61672-1(2005)中规定的声学计权,以考虑人耳的频率依赖性,或用于人体舒适性分析的各种频率计权,以考虑振动的感知,如ISO 8041(2005)、ISO 2631-1:(1997)和ISO 2631-5:(2004)中规定的计权。这样的计权通常应用于频域。然而,在某些情况下,也应用时域。
在这,我们仅为声学C计权滤波器为例来说明频率计权滤波器。C计权滤波器的滤波特性由标准IEC 61672-1(2005)定义。C计权滤波器在拉普拉斯平面上由位于20.6Hz和12200Hz的两个极点来定义,即s=−2π·20.6和s=−2π·12200,因为s的单位是rad/s。因此,如果我们分别用
来源:模态空间
作者:谭祥军












