自动驾驶漂移控制的研究有助于深入理解车辆极限运动控制机理,拓宽车辆的稳定操控极限,进一步开发具有专业驾驶员能力的自动驾驶技术,提高自动驾驶车辆的稳定性和安全性。与常规转弯不同,漂移是一种高侧滑角的专业驾驶行为,需要特定的触发条件,不能完全适应一般道路环境。相反,常规转弯没有限制。因此,研究使自动驾驶车辆同时具有漂移和常规转弯能力,对提高车辆在一般路径上行驶时的稳定性和安全性具有重要意义。
传统的轨迹跟踪控制器都是保证在复杂工况下的行驶安全并跟踪上车辆的参考横摆角速度,但是当车辆在高速行驶且紧急转弯时,可能会发生严重的失稳事故,车辆在这种极限情况下,车辆侧滑角会发生巨大变化,传统的稳定控制系统无法发挥作用。而赛车手常用的漂移技术可以使车辆在高速且大侧滑角下保持稳定状态。因此,可以通过控制车辆漂移来保证车辆在极限工况下的侧向稳定性。
通常情况下,稳态漂移工况的动力学特征为较大的侧偏角和横摆角速度、横摆角速度与方向盘转角方向相反以及轮胎力的高度饱和等。所谓稳态漂移,指车辆在漂移过程中保持相对稳定的控制输入和车辆状态,即动力学系统的平衡态。因此,车辆漂移是一个高度的非线性的复杂控制过程,本文使用车辆的3自由度非线性模型进行漂移控制研究。
1、车辆非线性动力学模型和轮胎模型
在漂移控制过程中,一般认为车辆姿态控制起到更加重要的作用。同时,在相图分析的过程中,二自由度整车动力学模型漂移平衡态的特征在三自由度整车模型中同样适用。因此,采用非线性的三自由度动力学模型。
三自由度车辆动力学模型为:

2、相图分析
相平面分析法是一个用来研究二阶系统稳定性的图示法,其基本概念很简单,就是在一个二阶动态系统的状态空间里生成一个对应于不同初始状态下的运动轨迹(也被称之为相平面的二维平面),然后根据这个二维图像来考察轨迹的特征。通过这种方法,系统的稳定性以及其他运动特征可以通过图像直观地获得。设,通过给定![]() 不同的初值,可得到时间t从0变化到∞的
不同的初值,可得到时间t从0变化到∞的![]() 的变化轨迹,此处速度为匀速,所以三自由度模型简化为二自由度模型,根据非线性二自由度动力学模型得到的相图(横轴为
的变化轨迹,此处速度为匀速,所以三自由度模型简化为二自由度模型,根据非线性二自由度动力学模型得到的相图(横轴为![]() 纵轴为
纵轴为![]() )如下所示:
)如下所示:
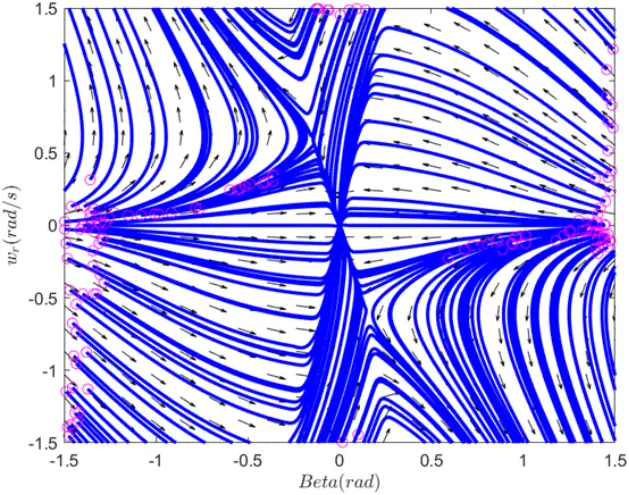
图1 ![]() 时的相平面图
时的相平面图
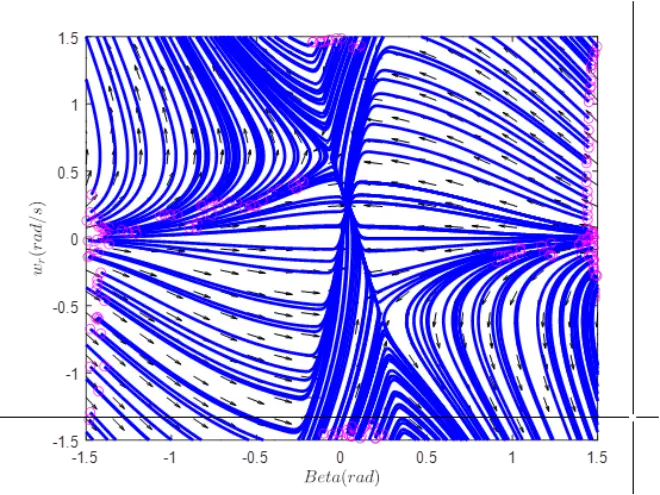
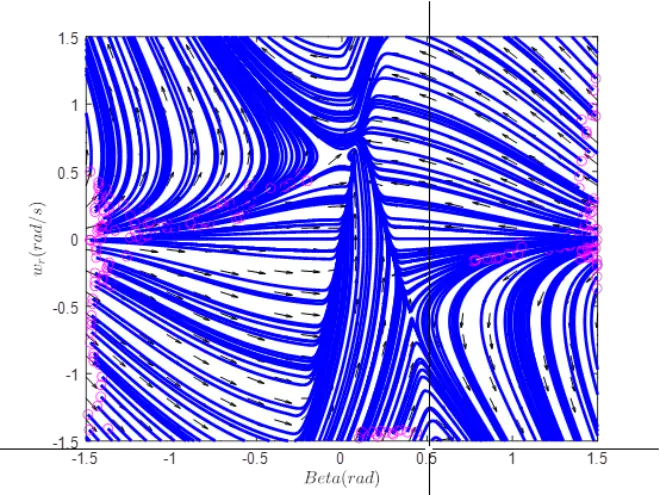
图3 ![]() 时的相平面图
时的相平面图
平衡点是给定β和wr初值后,β和wr随着时间的增加,轨迹都趋于0的点;鞍点是一个最终趋于0,另一个趋于∞大的点;不稳定点是两个都趋于∞的点。
在图1和图2中,即两种情况下,系统均存在三个平衡点,其中一个正常转弯工况平衡点(![]() 时为直线行驶工况)为稳定的平衡点,可以看到当系统的状态处于该点周围的时候,车辆状态会有靠近该点的趋势,此时系统状态处于稳定区内。当系统在该稳定平衡点上时,整个系统进入稳定平衡。另外两个漂移平衡点为不稳定的平衡点,当系统状态在该点周围时,会有远离该点的趋势,在该点的一侧系统的状态值会发散,而另一侧则会向稳定平衡点运动趋于稳定。漂移平衡点位于系统的稳定区和不稳定区的临界处,说明漂移状态是系统的临界稳定状态,这在理论上说明存在主动进入漂移的可能性,即通过控制可以使车辆从稳定状态运动到临界稳定状态然后进入漂移平衡点。
时为直线行驶工况)为稳定的平衡点,可以看到当系统的状态处于该点周围的时候,车辆状态会有靠近该点的趋势,此时系统状态处于稳定区内。当系统在该稳定平衡点上时,整个系统进入稳定平衡。另外两个漂移平衡点为不稳定的平衡点,当系统状态在该点周围时,会有远离该点的趋势,在该点的一侧系统的状态值会发散,而另一侧则会向稳定平衡点运动趋于稳定。漂移平衡点位于系统的稳定区和不稳定区的临界处,说明漂移状态是系统的临界稳定状态,这在理论上说明存在主动进入漂移的可能性,即通过控制可以使车辆从稳定状态运动到临界稳定状态然后进入漂移平衡点。
随着转角的逐渐增大,稳定节点向漂移平衡点移动的趋势会持续下去,直到稳定节点与漂移平衡点最终在第二象限“碰撞”,在这一点上,平衡相互湮灭,导致所谓的鞍点分叉。图3中,右侧漂移鞍点是系统的唯一平衡点,由于这种平衡是不稳定的,因此没有状态轨迹会收敛到稳定的平衡点,车辆只能通过漂移的方式实现过弯运动。
3、漂移平衡点分析
漂移平衡点是相平面图中的鞍点,根据车辆的三自由度动力学模型表达式,稳定平衡点和鞍点通过状态量变化率等于零的方式可以进行求解,将求解的数值通过图像方式对比稳态转弯平衡和稳态漂移平衡。此时,后轮横向力的公式变为:
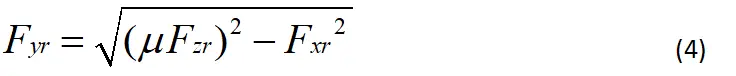
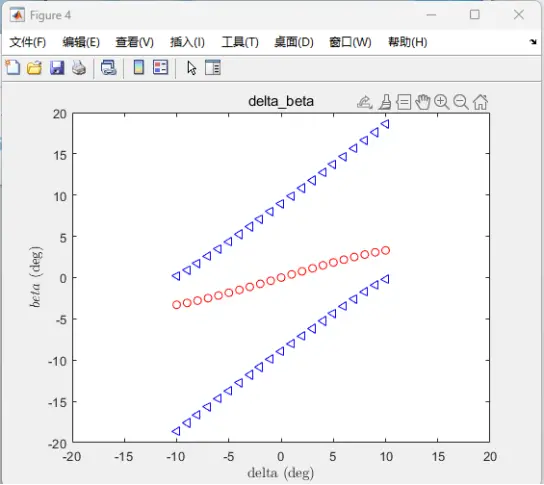
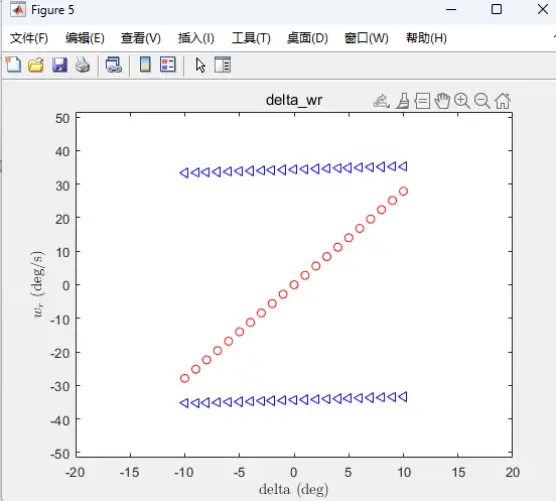
图5 系统平衡状态下的前轮转角-横摆角速度
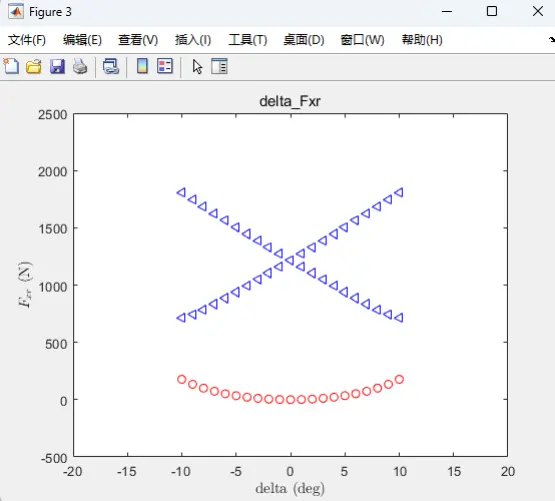
图6 系统平衡状态下的前轮转角-后轮纵向力
上图给出了当给定纵向车速![]() 时,当前轮转角不断在范围内变化时,车辆所处的平衡点的前轮侧向力、后轮纵向力、后轮侧向力、后轮胎力、横摆角速度以及质心侧偏角的变化情况。由上图可知,当车辆处于稳态转向运动平衡状态时,车辆的质心侧偏角
时,当前轮转角不断在范围内变化时,车辆所处的平衡点的前轮侧向力、后轮纵向力、后轮侧向力、后轮胎力、横摆角速度以及质心侧偏角的变化情况。由上图可知,当车辆处于稳态转向运动平衡状态时,车辆的质心侧偏角![]() 趋近于零,此时车辆处于稳态平衡,图中的o号代表稳定的平衡点,D号代表不稳定的漂移平衡点(横摆角速度大于零表示左漂移平衡点,小于零表示右漂移平衡点)。我们可以从图中看出,车辆在非稳定平衡态时。以车辆的前轮转角为正为例,此时,车辆的质心侧偏角为正,车辆的横摆角速度为负,该表现证实了车辆处于漂移平衡态时,车辆的前轮转角反打,同时由图可知,后轮胎力达到饱和。
趋近于零,此时车辆处于稳态平衡,图中的o号代表稳定的平衡点,D号代表不稳定的漂移平衡点(横摆角速度大于零表示左漂移平衡点,小于零表示右漂移平衡点)。我们可以从图中看出,车辆在非稳定平衡态时。以车辆的前轮转角为正为例,此时,车辆的质心侧偏角为正,车辆的横摆角速度为负,该表现证实了车辆处于漂移平衡态时,车辆的前轮转角反打,同时由图可知,后轮胎力达到饱和。
4、定圆漂移控制仿真
车辆漂移时,需要将车辆状态稳定在平衡点,使得车辆维持“大的质心侧偏角、方向盘反打”的状态,通过控制油门和转向来使后轮胎达到饱和状态。理论上,将车辆的状态直接控制到平衡点,即可实现车辆的漂移。专业赛车手在漂移竞赛中通过有意使车辆处于过度转向状态,使后轮或全部轮胎处于全滑状态,并精确控制油门与转向,不仅能够实现稳态漂移过弯同时还能实现精确的路径跟踪。
4.1 基于三自由度模型的NMPC定圆漂移控制
表1所示为vx=8m/s时的漂移平衡点信息。控制策略:车辆初始车速10m/s,先通过制动使车辆达到漂移状态,在通过车速低于8m/s切换漂移控制器。
表1 vx=8m/s时的漂移平衡点信息

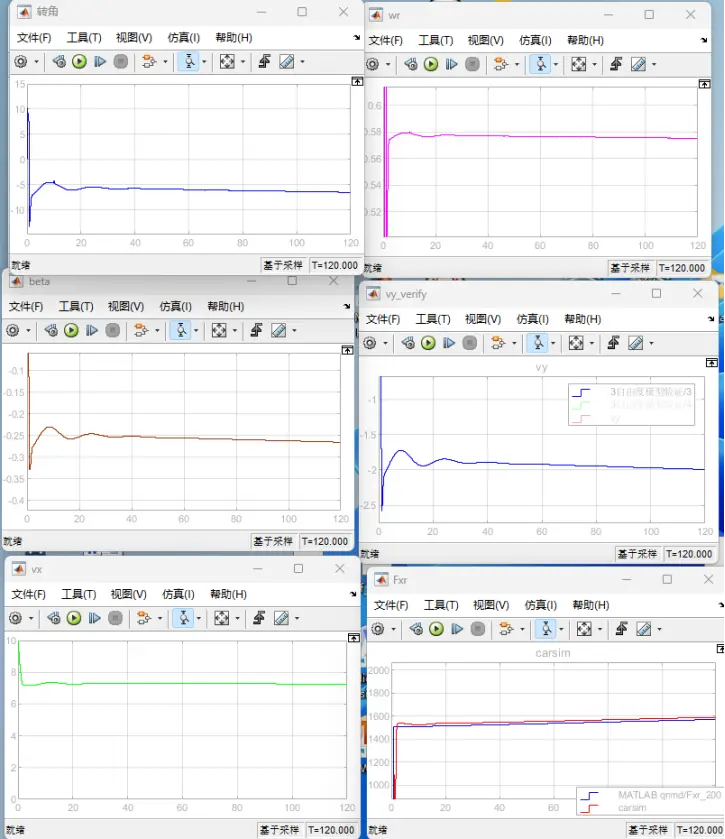
图7 前轮转角=-5deg时的定圆漂移
(图中依次为前轮转角(deg)、横摆角速度wr(rad/s)、质心侧偏角beta(rad)、横向速度vy(m/s)、纵向速度(m/s)和后轮纵向力Fxr(N)的曲线图)
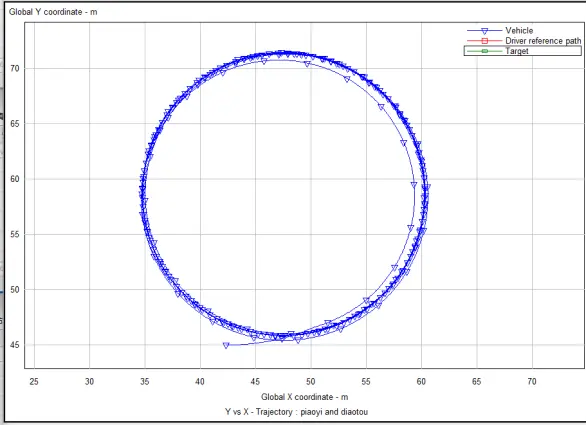
图8 前轮转角=-5deg时定圆漂移的实际路径
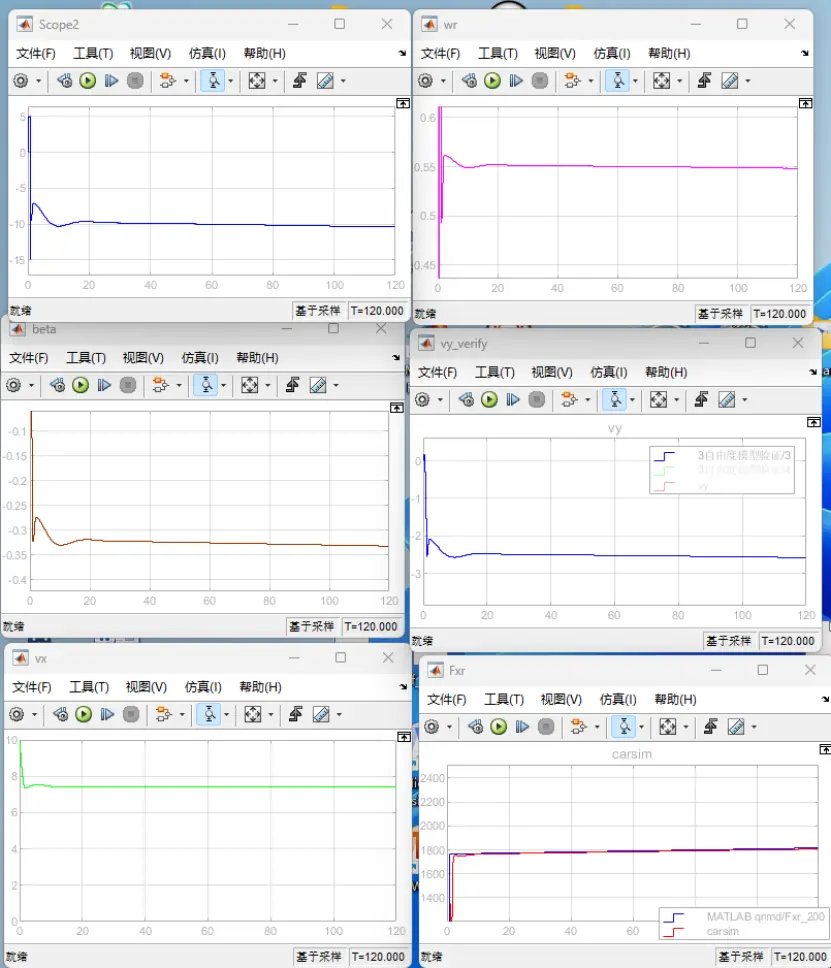
图9 前轮转角=-10deg时的定圆漂移
(图中依次为前轮转角(deg)、横摆角速度wr(rad/s)、质心侧偏角beta(rad)、横向速度vy(m/s)、纵向速度(m/s)和后轮纵向力Fxr(N)的曲线图)
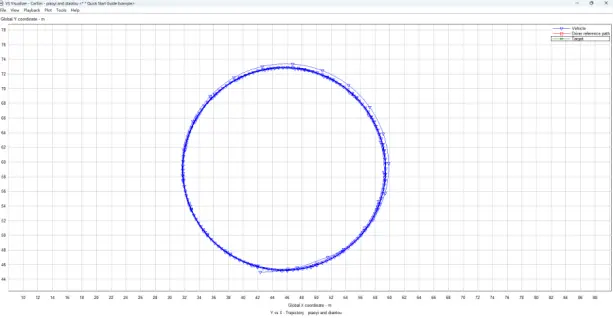
图10 前轮转角=-10deg时定圆漂移的实际路径
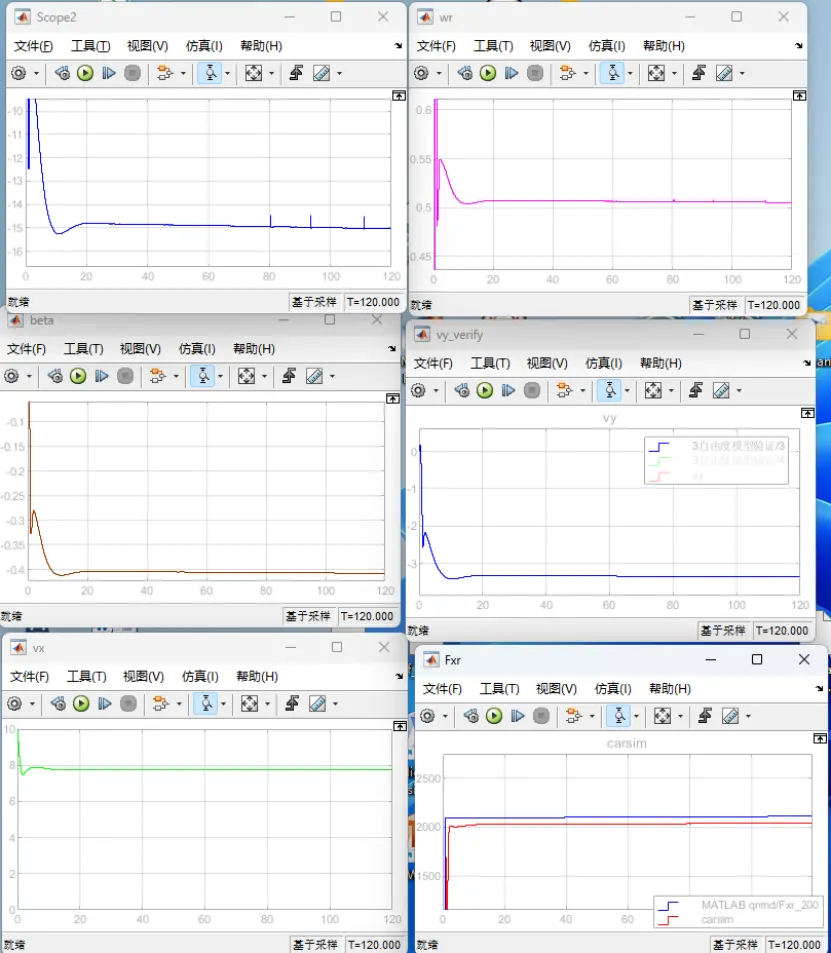
图11 前轮转角=-15deg时的定圆漂移
(图中依次为前轮转角(deg)、横摆角速度wr(rad/s)、质心侧偏角beta(rad)、横向速度vy(m/s)、纵向速度(m/s)和后轮纵向力Fxr(N)的曲线图)
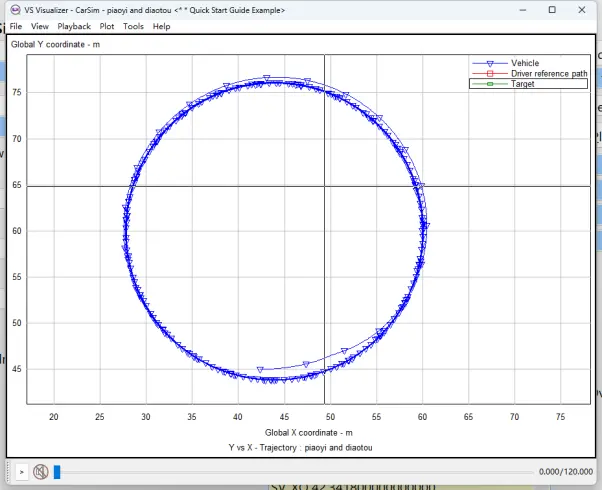
图12 前轮转角=-15deg时定圆漂移的实际路径
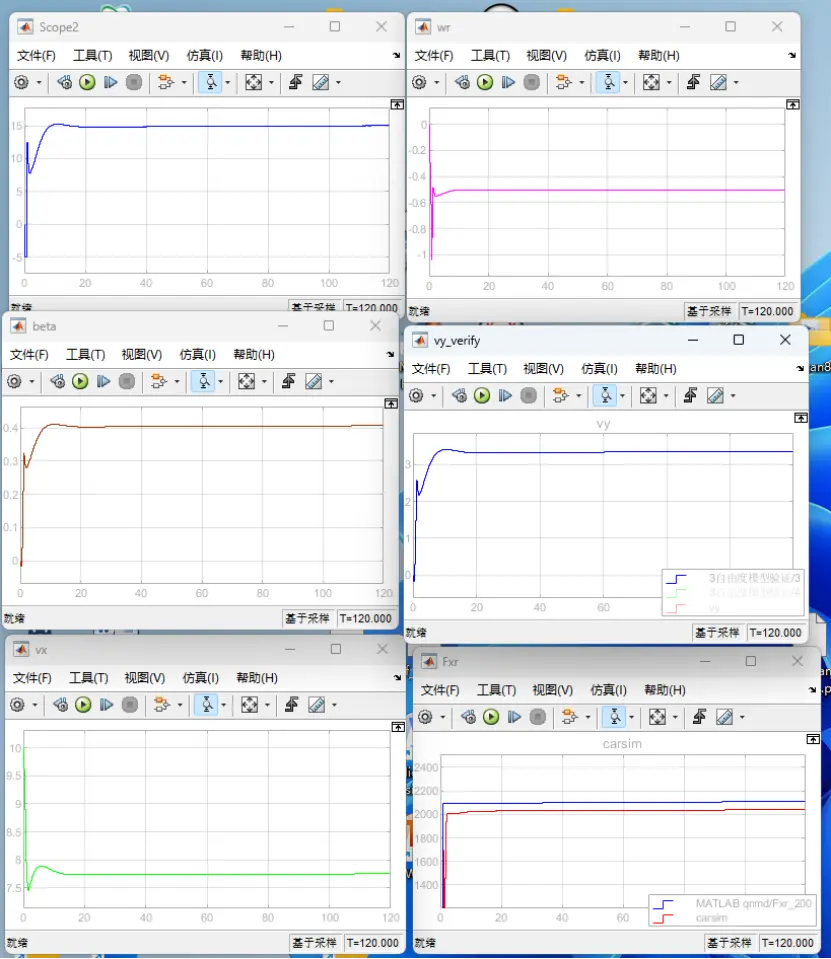
图13 前轮转角=15deg时的定圆漂移
(图中依次为前轮转角(deg)、横摆角速度wr(rad/s)、质心侧偏角beta(rad)、横向速度vy(m/s)、纵向速度(m/s)和后轮纵向力Fxr(N)的曲线图)
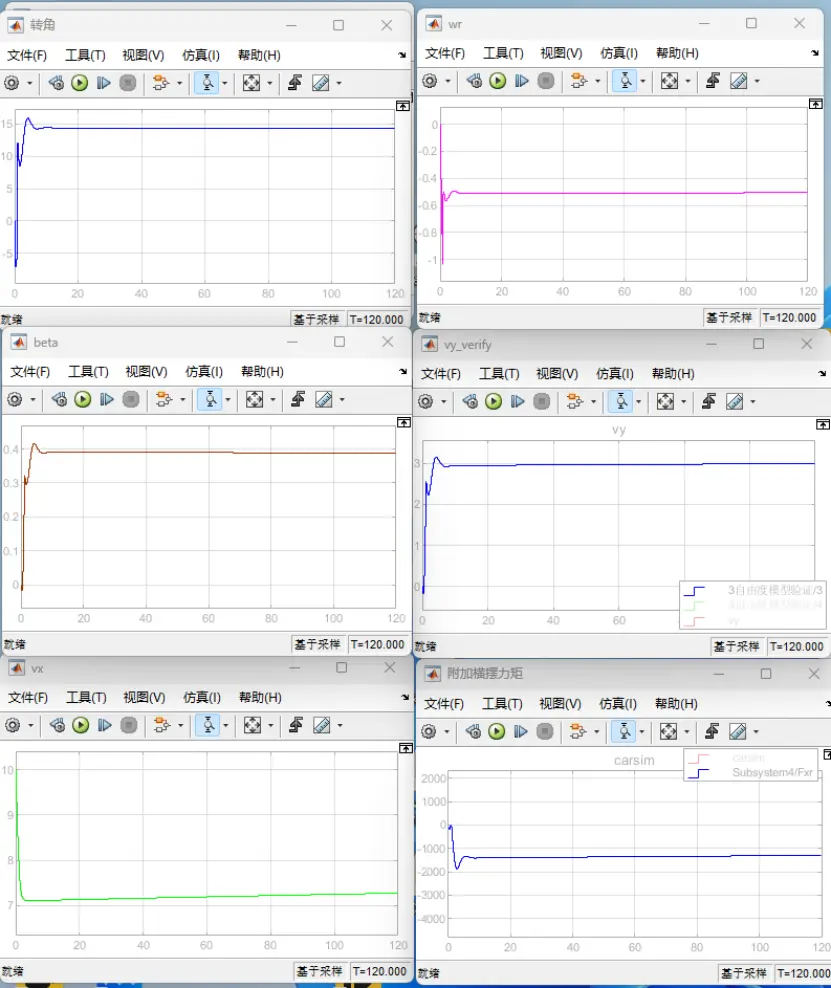
图14 前轮转角=15deg时定圆漂移的实际路径
4.2 基于二自由度模型的分布式驱动的NMPC定圆漂移控制器
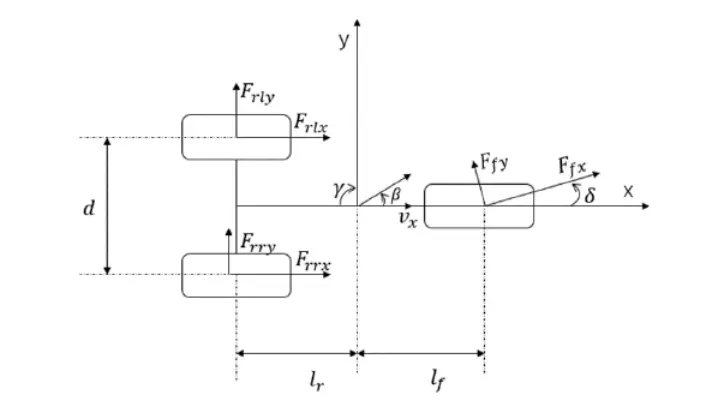
图15 三轮模型
由于车辆为后轮分布式驱动,前轮没有施加转矩,故前轮可视为一个轮胎。基于等效假设的三轮模型的非线性车辆动力学方程如下所示:
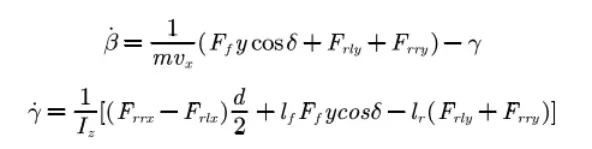
4.2.1 控制策略1
车辆初始车速10m/s,先通过制动使车辆达到漂移状态,在通过车速低于8m/s切换漂移控制器。
1. 横向控制:对二自由度模型增加附加横摆力矩,附加横摆力矩是因为左后轮和右后轮分配的扭矩不平衡产生的。
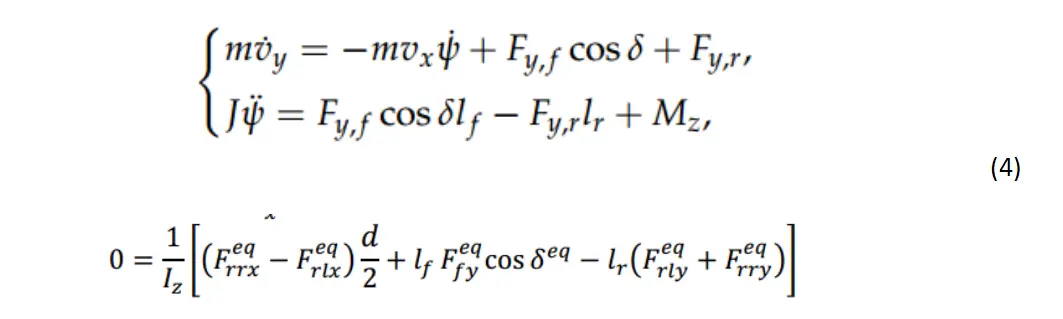
通过控制算法得到需要的前轮转角d和附加横摆力矩Mz。
2. 纵向控制:通过pid算法和电机模型得到保持匀速需要的总扭矩。
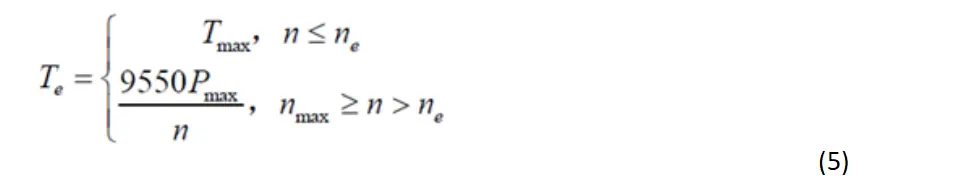
Pmax取电机的额定功率。
附加横摆力矩分解为左右轮的纵向力:Mz=Bw/2*(Fxrr-Fxrl)
考虑轮胎动力学:
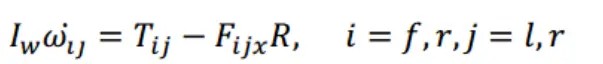
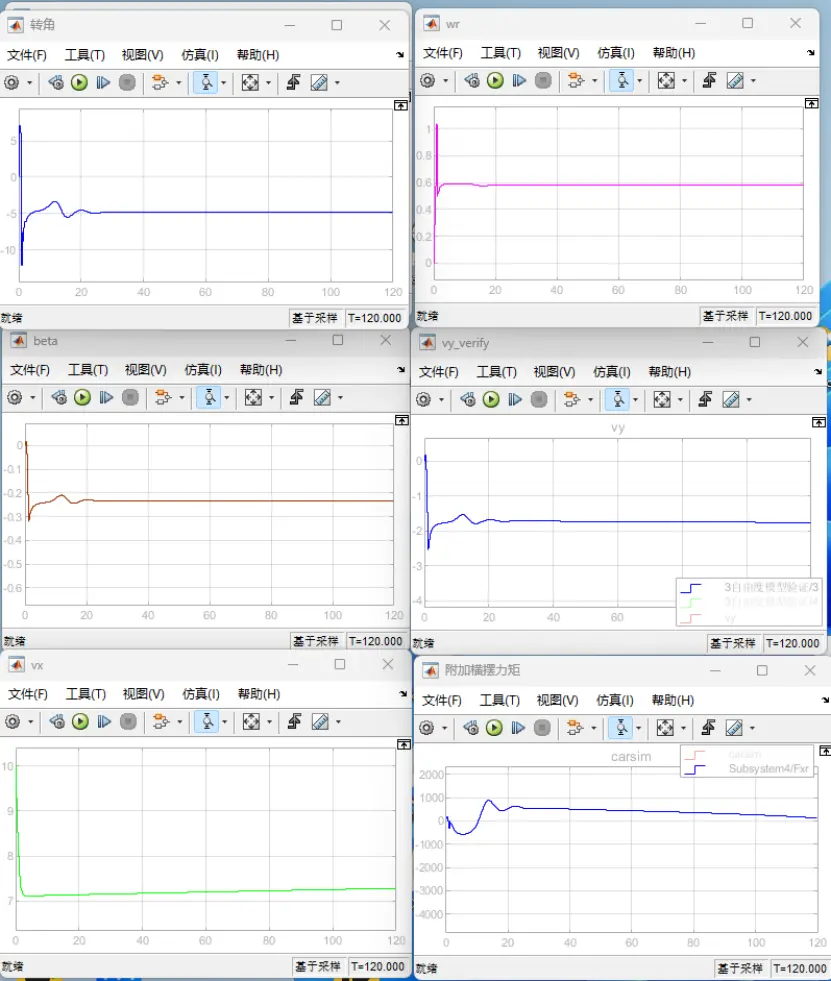
图16 前轮转角=-5deg时的定圆漂移
(图中依次为前轮转角(deg)、横摆角速度wr(rad/s)、质心侧偏角beta(rad)、横向速度vy(m/s)、纵向速度(m/s)和附加横摆力矩Mz(N)的曲线图)
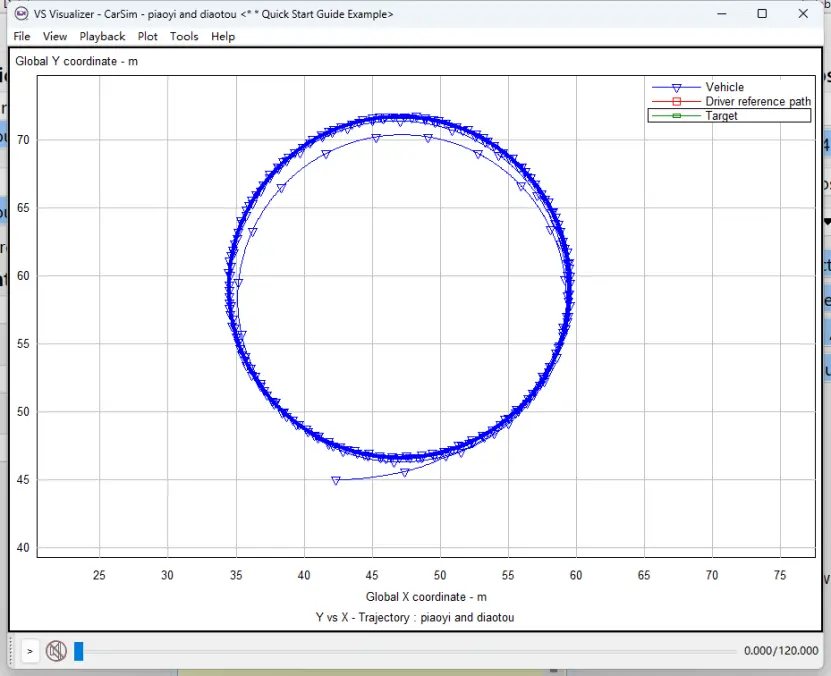
图17 前轮转角=-5deg时定圆漂移的实际路径
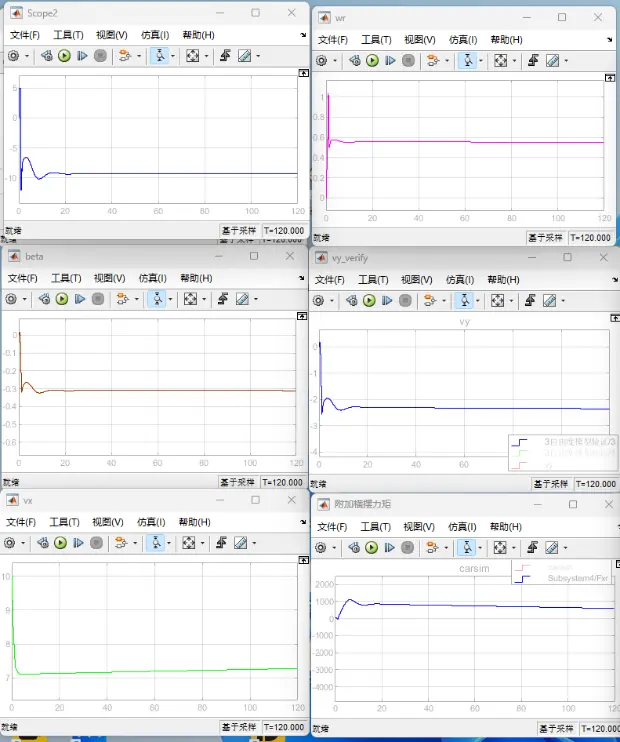
图18 前轮转角=-10deg时的定圆漂移
(图中依次为前轮转角(deg)、横摆角速度wr(rad/s)、质心侧偏角beta(rad)、横向速度vy(m/s)、纵向速度(m/s)和附加横摆力矩Mz(N)的曲线图)
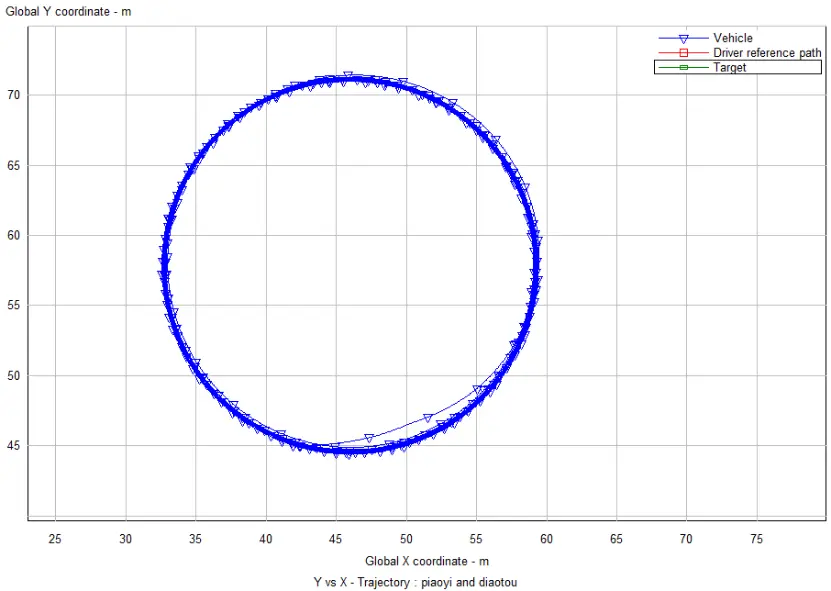
图19 前轮转角=-10deg时定圆漂移的实际路径
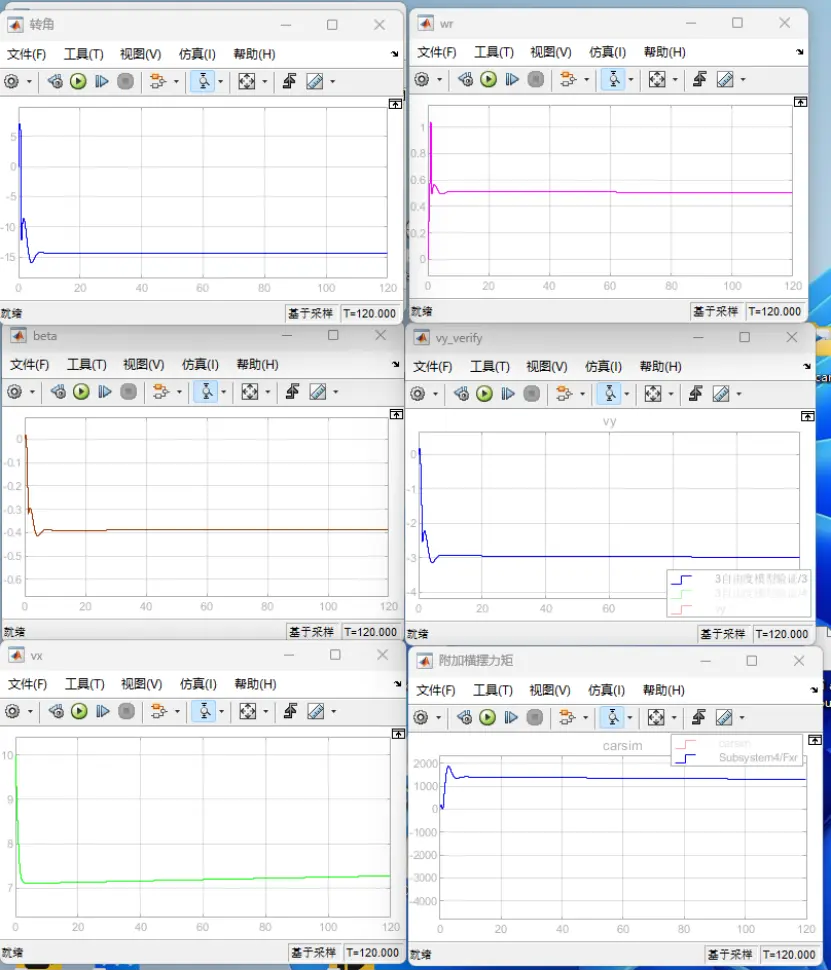
图20 前轮转角=-15deg时的定圆漂移
(图中依次为前轮转角(deg)、横摆角速度wr(rad/s)、质心侧偏角beta(rad)、横向速度vy(m/s)、纵向速度(m/s)和附加横摆力矩Mz(N)的曲线图)
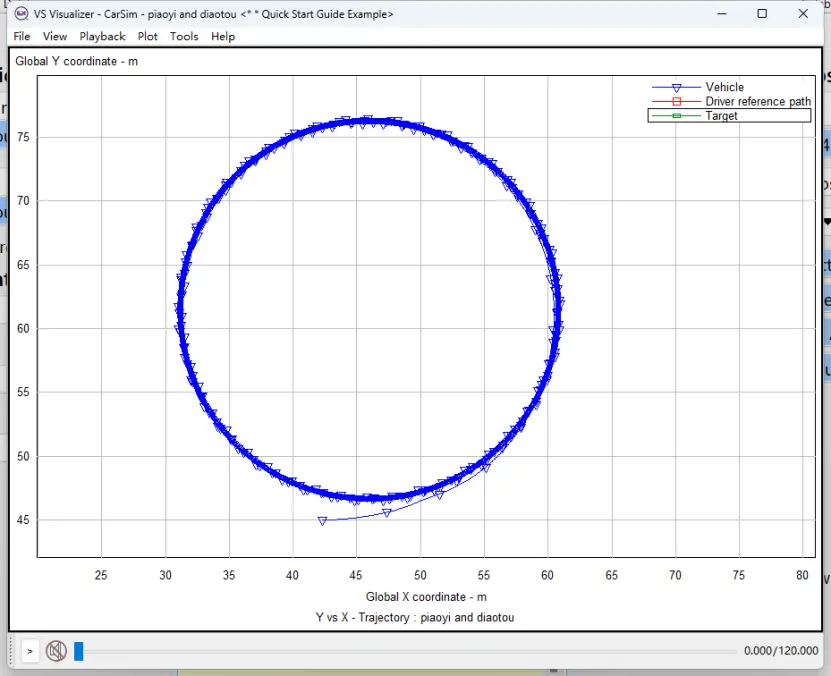
图21 前轮转角=-15deg时定圆漂移的实际路径

图22 前轮转角=15deg时的定圆漂移
(图中依次为前轮转角(deg)、横摆角速度wr(rad/s)、质心侧偏角beta(rad)、横向速度vy(m/s)、纵向速度(m/s)和附加横摆力矩Mz(N)的曲线图)
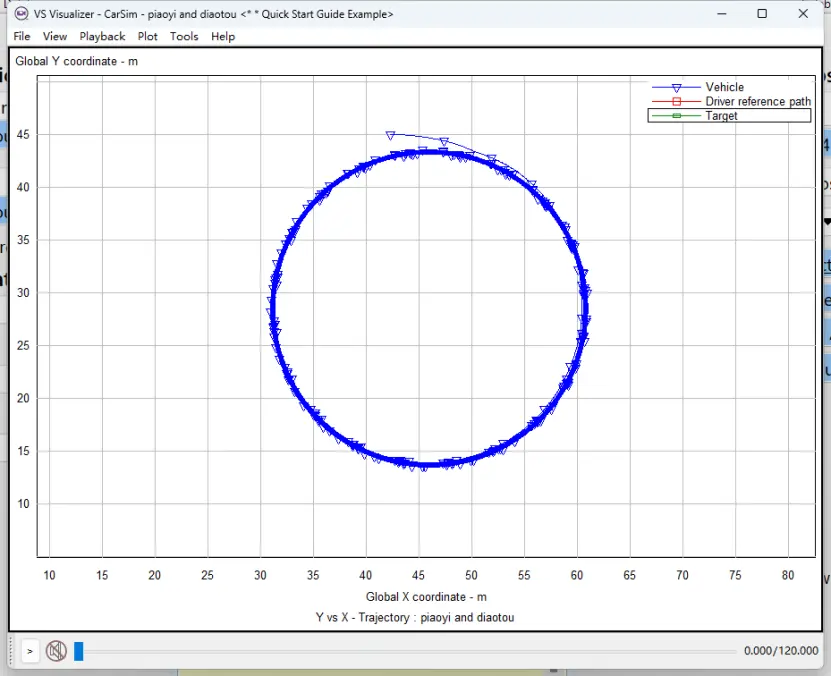
图23 前轮转角=15deg时定圆漂移的实际路径
4.2.2 控制策略2
直接从8/m/s的匀速开始漂移控制器直接追踪鞍点控制车辆完成漂移。
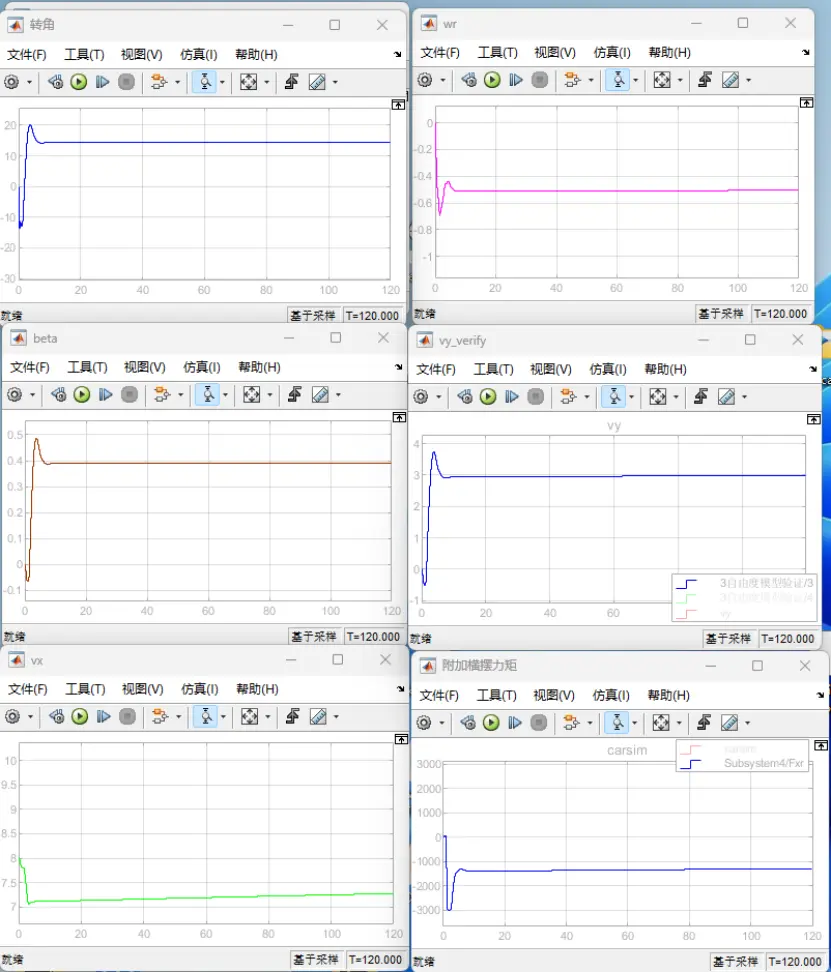
图24 前轮转角=15deg时定圆漂移的实际路径
(图中依次为前轮转角(deg)、横摆角速度wr(rad/s)、质心侧偏角beta(rad)、横向速度vy(m/s)、纵向速度(m/s)和附加横摆力矩Mz(N)的曲线图)
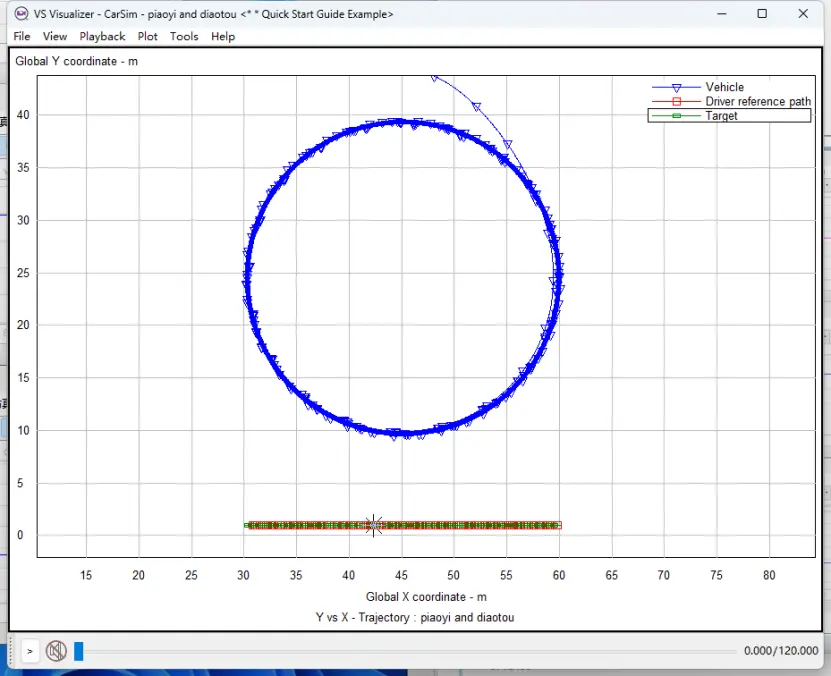
图25 前轮转角=15deg时定圆漂移的实际路径
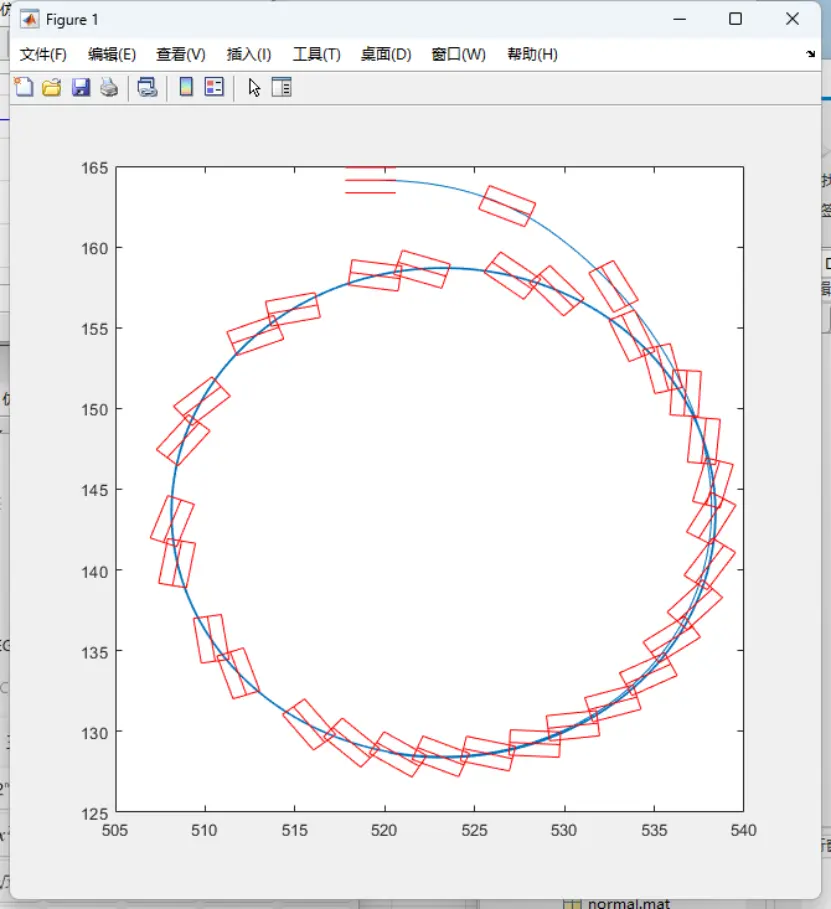
图26 定圆漂移实际行驶轨迹
来源:智能运载装备研究所












