在不失一般性的前提下,我们首先研究了TTS车身与第个障碍物之间的无碰撞条件。为简单起见,将TTS的第个物体视为矩形(),将第个障碍物视为多边形避碰条件可表示为:
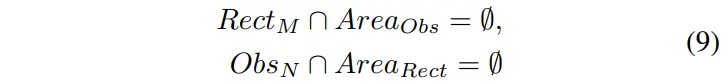
其中,,式(9)明确了确定TTS无碰撞条件的标准:
-
TTS体的每个顶点都在障碍物之外。
-
障碍物的每个顶点都在TTS体之外。
这个结论可以推广到任意的TTS体和任意的障碍物。注意,当扩展到多体时,应避免系统的内部碰撞。因此,TTS的避碰约束可进一步表示为:
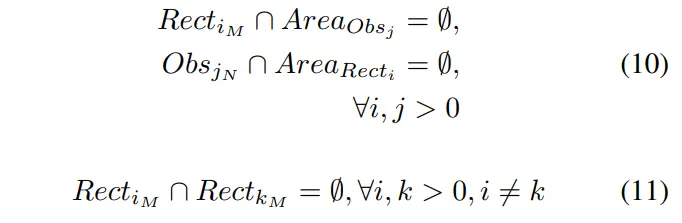
其中和分别表示第个物体和第个障碍物的顶点。和分别表示第个物体和第个障碍物被占据的面积。TTS相关参数的符号和定义见表1。
表1. TTS的参数定义。

3 混合A*-跳点搜索规划
我们的主要算法框架遵循混合A,[19]并对其进行了详细的修改。如第1-B节所述,我们的方法受到了跳跃点搜索(Jump Point Search, JPS)算法的启发,其核心概念是有选择地扩展网格图上的某些节点[7]。JPS包括两个主要原理:邻居剪枝和跳点识别。但是JPS是传统A的扩展,没有考虑车辆的运动学,生成的路径不能被车辆执行。因此,我们借鉴上述两种JPS的核心思想,并将其应用于改性混合动力A* (MHA)的改进。具体而言,做了以下更改:
-
考虑到TTS是一个欠驱动系统,倒车对经验丰富的人类驾驶员来说尚且是挑战,更不用说无人驾驶汽车。因此,我们指定了一个相对较高的倒车成本。此更改的主要目的是最大程度地避免对TTS进行不必要的反转。如图1所示,从TTS后部展开的绿线(左)和红线(右)表示MHA和HA-JPS向后展开的成本不同(红线表示成本较高)。通过减少节点向后展开的可能性,进一步保证了机动过程的安全性和平稳性。
-
展开节点时,优先展开与当前TTS状态方向角度相同的方向,保证轨迹平滑。如图1右半部分所示,搜索代价随着迭代次数的增加而增加(绿-褐-红),而保持当前角度的节点与所属集群相比颜色较浅。
-
如果搜索空间是开放的,即包含更多的潜在可行方向,我们有目的地扩大TTS转向角度阈值的采样间隔以提高搜索速度。在搜索空间变窄的同时,缩短采样间隔以保证搜索精度。如图1右半部分所示,随着距离障碍物越近,采样间隔越密集。
算法1给出了HA-JPS的总体算法框架:

来源:同济智能汽车研究所












