本文认为正常驾驶环境下、车辆在两个方向上受到多种作用力(包括随机力,例如路面的随机激励、驾驶员随机误差等),从而产生车辆的运动轨迹(也即2D坐标、速度、加速度)。车辆受到的作用力列表如所图 4示。反常驾驶行为通过修改作用力的表达形式、添加某些项(如后文模型的chaotification项)或者忽略某些力来实现(Qi, 2024)。对图 4进行进一步说明,(1)图 4-b中,可以认为车辆受到中心线的吸引力。当吸引力较弱、车辆行为表现为车道内随机侧向波动;(2)图 4-c中,车辆会对相邻车道的车辆造成两个方向的压力,这个2D压力在交通流中向上游传导。半椭圆为车辆受作用的半径,其大小随着车辆速度变化而变化。
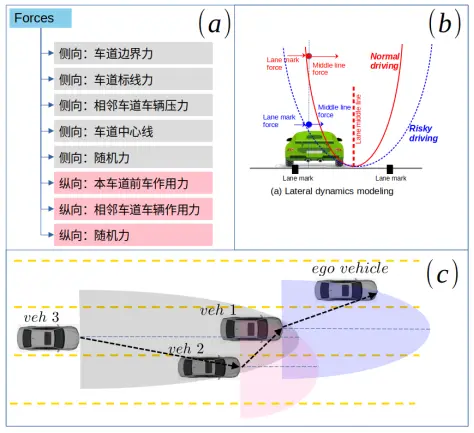
图 4 两个方向上的作用力
假设车辆(第i辆车)的状态向量为[xi,ui,zilon,yi,vi,zilat],表示车辆的纵向坐标、纵向加速度、纵向噪音、侧向坐标、侧向速度、侧向噪音(如轮胎的随机侧向力等)。本车(也即车辆i)的前方车辆坐标为Xle(i)(le表示leader)、周围车辆的集合为ne(i)(“ne”表示neighbor)。正常驾驶模型如图 5所示。
本模型采用带跳跃项的随机微分方程。采用这一技术路线的原因如下:(a)该类模型很容易和已有微观交通仿真软件相结合。(b)模型中众多参数可解释、可调节,适合描述不同的反常行为。模型的形式复杂、但结构简单。结构的解读如图 5所示。图5(a)~(c)为纵向运动、图5(d)~(f)为侧向运动。图5(c)和(f)为随机过程,表示纵向噪音和侧向噪音。在图5中,噪音的形式为OU过程,也可以替换为其他随机过程,例如几何布朗运动(Yuan et al. 2019)、分数阶布朗运动(Wang et al. 2010)等。
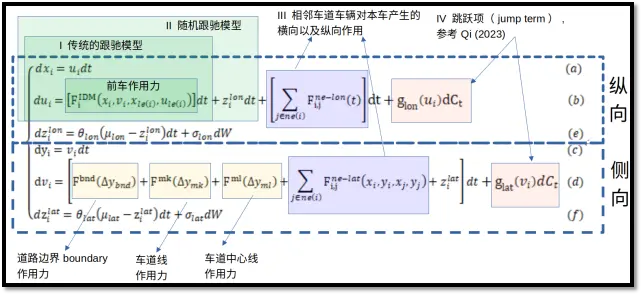
图 5 模型结构
图5中,I部分(传统跟驰模型)中的前车作用力采用IDM模型,也可以替换为其他任意跟驰模型;II部分是随机跟驰模型,类似已有的随机纵向模型(Yuan et al. 2019);III部分是侧向车道的车辆对本车道车辆产生的纵向力,例如,相邻车道的车在压线行驶时、对本车的作用力。该作用力表达式见图6、推导过程见(Qi, 2024b)。IV部分是跳跃项,用来解释较大的侧向和纵向急动度(Wang, Khattak, Liu et al, 2015)。
图 6 相邻车道的车辆对本车的2D作用力
(Qi, 2024a)(Qi, 2024b)
对于各侧向作用力,其表达式如下:
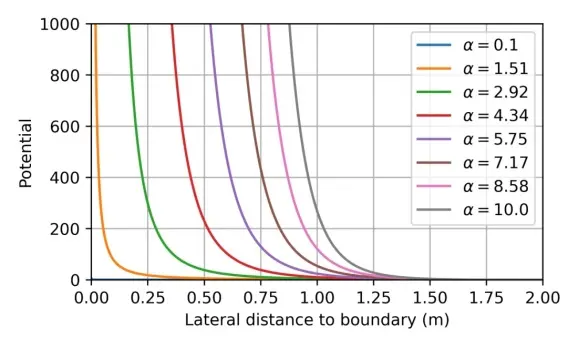
● 道路边界作用力fbnd(△ybnd),随着车辆和道路边界距离△y递增至无穷(这一属性是假设车辆永远不会穿越至道路边界线外),公式如Eq.1、曲线形式如图7左图;
● 车道线作用力fmk(△ymk)。作用力随着车辆与车道线之间的距离△y而变化。公式如Eq.2所示、曲线形式如图7右图。该公式的基本思想:当车辆接近车道线时、作用力增加,但是车辆跨越车道线之后、又降低;
● 车道中心线吸引力fml(△yml)。可以采用抛物线,如图 4-b所示,此处不再赘述。
来源:sasetech
作者:祁宏生












