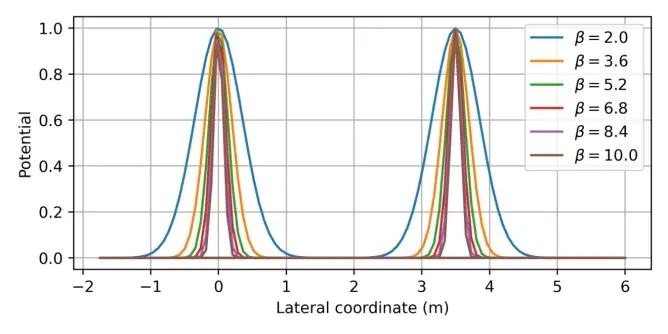
图 7 道路边界作用力
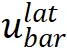
Eq.1
Eq.2
3.3 模型架构：反常驾驶模型
图5表达了正常驾驶行为受到的力。对公式各项进行修改、就得到了反常驾驶行为模型。依照图3列出的反常行为，对图5中的具体项进行修改如下:
● A1前车感知。在图5中前车的实时坐标为xle(i)(t)。反常驾驶环境下，驾驶员无法准确感知该坐标，从而可用函数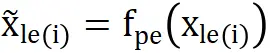
表达不准确的前车感知位置
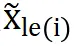。假设在时间段[t0dist1dis]内分心，则感知的前车轨迹可以表达为下式：
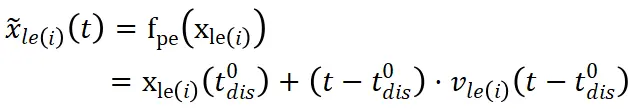
Eq.3
● A2均衡状态。在纵向控制（也即图5公式b）中添加混沌控制项uchaos(t)。考虑混沌控制项后、纵向驾驶形式上表达为dui=...+uchaos(t)。该项如Eq.4所示（Chen, 2003）。
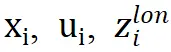
Eq.4
● B1: 车道/道路的感知（酒驾/醉驾/路怒等）。对真实的车辆与道路边界、车道线和车道中心线的距离（△ybnd、△ymk、△yml）进行修改，例如，假定车辆与车道线的真实距离为△yml、醉驾情况下的感知误差为Zdrunk，则驾驶员决策所依据的与车道线距离表达为△yml+Zdrunk。图8表示真实道路和感知道路的区别。在下节对其进行数值仿真。
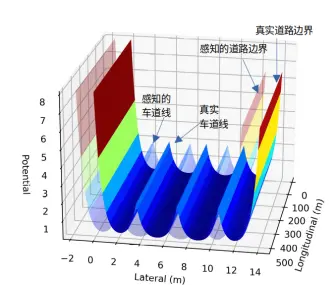
图 8 侧向感知反常
● B2缺乏明确的侧向目标位置。例如分心驾驶。在图 5直接公式d中舍弃车道中心线的吸引力项Fml(△yml)。
● B3侧向较大波动。可以通过增大侧向噪音的参数来实现（也即增大图 5公式f中的σlat）。
● B4完全侧向自由运动。舍弃在图5直接公式d中所有侧向力（保留Fbnd(△ybnd)，以避免车辆行驶至道路范围之外）。
当考虑上述反常因素时，模型产生的行为就不能精确控制。为了控制模型产生轨迹的风险水平（例如，不能让车辆之间产生碰撞，毕竟本文模型是反常驾驶行为模型、不是交通事故模型），提出控制屏障函数（control barrier function）、调节风险水平（图3中的Block B）。在纵向控制公式（图5公式b）中添加纵向控制项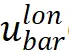
（lon表示longitudinal、bar表示barrier）、在横向公式（图5公式e）中添加侧向控制项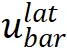。以纵向为例，添加控制项之后的形式如Eq.5所示。
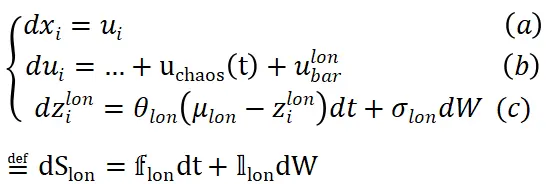
Eq.5
添加控制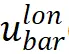
的目的是将纵向风险水平维持在一定的水平。假定我们想让模型产生的轨迹的风险水平（和周围车辆的距离）维持在
以上，定义该风险水平为一集合
：
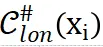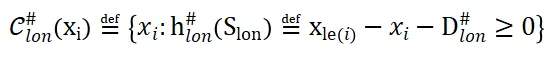
Eq.6
其中，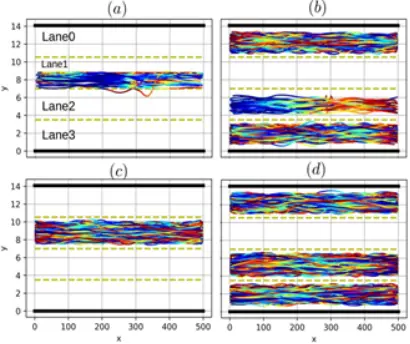
为依赖于Slon（也即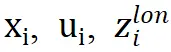）的函数。则按照随机控制屏障函数理论（Clark ,2021），当对于任意Slon、满足下述条件时候，
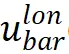会使系统维持在集合
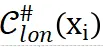内。
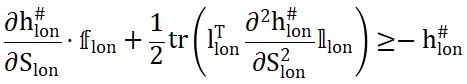
Eq.7
以上述不等式为约束、最小化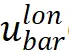和参考控制量（uchaos(t)）之间的差距，可以得到相应的控制量
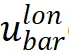、代入Eq.5，得到车辆的轨迹（Qi, 2024b）。
3.4 部分反常驾驶行为的数值仿真
本部分对几种常见的反常驾驶行为进行数值仿真。
3.4.1 侧向随机波动
侧向随机波动通过调节σlat来实现。图9-c给出了仿真结果。仿真场景包括4条车道。车道1的参数σlat是车道2车道0、2、3的参数取值的两倍。图9-c为车道1的2d轨迹；图9-d是其余车道的2d轨迹。图9-a为highD的侧向位置的std（车辆和本车道中心线的距离的标准差。“11_tracks”是highD数据文件的文件名）；图 9-b是4条车道的std。可见，模型可以刻画大幅度波动。
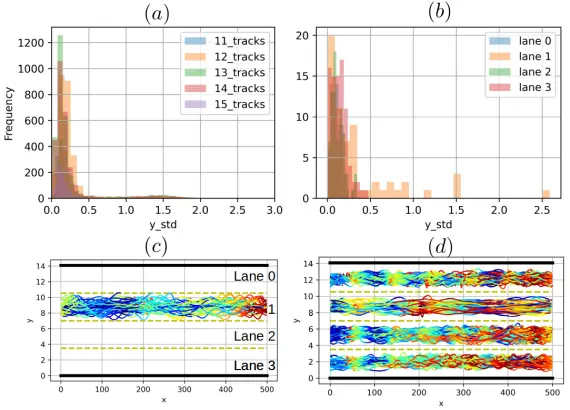
图 9 (a): highD 数据集; (b) 仿真结果;
(c): 反常驾驶车辆，σlat=0.4; (d) 正常驾驶车辆hσlat=0.2
来源：sasetech 作者：祁宏生
