最简单的模拟滤波器是1阶滤波器,对于一个低通滤波器而言,它有如下的滤波特性
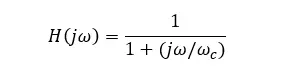
式中,ωc是滤波器的截止频率。一阶低通滤波器在电子器件中很常见,尽管在振动设备中,一阶高通滤波器可能更常见,但它包括在许多传感器和信号调节单元中。
1阶高通滤波器的特性为
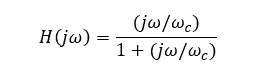
它的幅频响应(增益)为
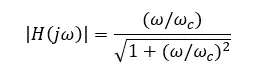
最常见的通用滤波器是巴特沃斯滤波器,对于巴特沃斯低通滤波器而言,它的滤波增益为
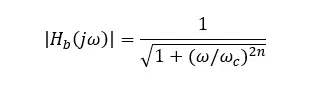
式中,整数n称为滤波器阶数。前面讲过,滤波器的阶数决定了滤波器过渡带的渐近斜率,同时也会影响其他方面,如时间延迟、瞬态响应等。当n=1时,巴特沃斯1阶低通滤波器与前面最简单的1阶低通滤波器相同。巴特沃斯滤波器是一个有用的滤波器,是因为它具有最大的平坦增益特性和相对线性的相位特性。因此,在许多应用中经常使用它,例如,在已标准化的倍频程和1/3倍频程滤波中,使用的是3阶巴特沃斯滤波器。
设计模拟滤波器需要有特定的硬件,如常见的电阻、电容、电感、集成运算放大器等元器件。在模拟电路中,元器件或主动或被动地改变信号,根据这一特性,模拟滤波器分为被动和主动滤波器。被动型滤波器也称为无源滤波器,由被动元器件(电阻、电容、电感等)组成;主动型滤波器也称为有源滤波器,包含集成运算放大器等主动元器件,支持增益控制和高阶滤波等功能。
模拟滤波器是对模拟信号进行滤波的滤波器,在早期,较普遍,而在数字时代,数字滤波器更为普遍。但在特定的应用场合仍然使用模拟滤波器,如信号测量过程中的AC耦合高通滤波器和抗混叠滤波器均是模拟滤波器。
07
—
数字滤波器
在分析振动噪声数据时经常使用数字滤波器,例如,在进行频域分析或声学倍频程和1/3倍频程滤波分析,人体振动计权(舒适性)或冲击响应谱分析之前,通过滤波减少信号的带宽。数字滤波器及其设计在数字信号处理领域中是一门独立的学科,因此,在这里,我们将只从用户应用的角度来描述一些简单的方面,使你对数字滤波器有一个基本的了解。
数字滤波器输入xn与输出yn之间的一般定义如下:
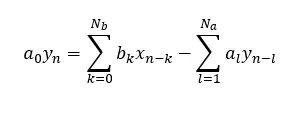
式中,滤波器系数al和bk定义了滤波器的特性。如果Na为零,即滤波器仅使用之前的输入来计算输出(没有上式中的第二项),则该滤波器称为有限脉冲响应(FIR)滤波器,因为它的FIR长度为Nb+1(滤波器的阶数或系数项)。另一方面,如果滤波器中有非零系数al,则称为无限脉冲响应(IIR)滤波器。IIR滤波器阶数由Nb+1和Na决定。IIR滤波器计算当前输出除了使用输入计算输出之外,还要使用之前的输出计算当前的输出,这使得IIR滤波器具有递归特性,因此,有时IIR滤波器也称为递归滤波器。两类数字滤波器名称中均有“脉冲响应”一词,是指滤波器频响在时域中的外形像脉冲,因为通常滤波器有宽带的频率响应,这在时域上对应短时脉冲,如图14所示。
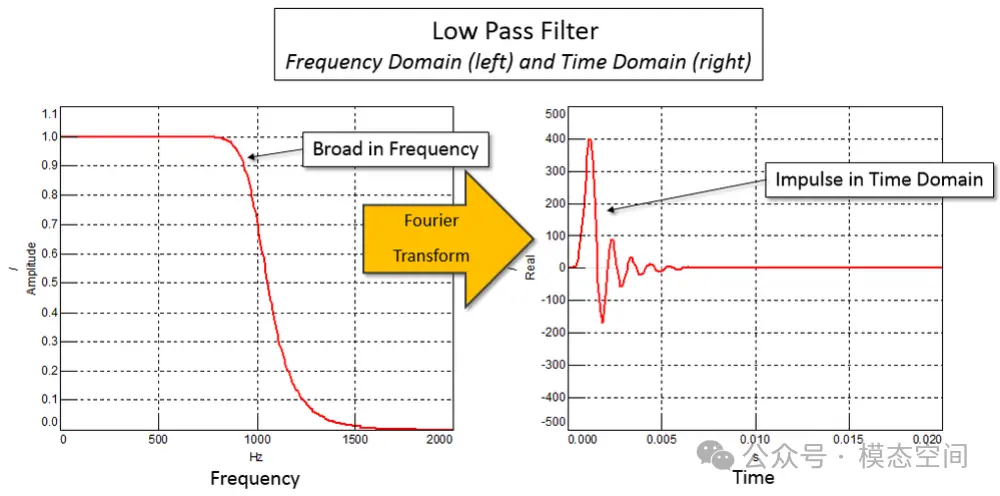
图14 低通数字滤波器在频域(左)和时域(右)中的形状
IIR滤波器的优点在于,对于与FIR相似的滤波器过渡带衰减斜率,可以使用较低阶或较少数量的系数项,即可以实现更强大的滤波器特性。这意味着需要更少的计算来实现相同的结果,使IIR的计算速度更快。然而,IIR具有非线性相位和稳定性问题。这有点像龟兔赛跑的寓言。FIR滤波器就像赛跑中的乌龟——缓慢而稳定,总能跑完全程。兔子就像IIR过滤器——非常快,但有时会崩溃,无法完成比赛。虽然IIR滤波器通常比FIR滤波器更具时间效率,可能是首选的数字滤波器。然而,在某些特殊情况下,首选FIR滤波器,特别是需要线性相位特性时,这一点将在下面讨论。
由前面的公式知道,对于FIR滤波器而言,数字Nb越大,滤波器的阶数越高。换句话说,公式中包含的系数项越多,例如,如果滤波器中有10项,而不是5项,那么,滤波器计算将花费两倍的时间。另一方面,包含越多的系数项(阶数),滤波器的过渡带衰减斜率越陡峭,计算必然要花费更长的时间,这也对时间延迟有影响。
如图15所示,对于相同的阶数,FIR滤波器和IIR滤波器的过渡带衰减斜率有很大的不同。由于IIR滤波器的递归特性,其中部分滤波器输出用作输入,使得在相同阶数的情况下,IIR滤波器可以实现更陡峭的衰减。相反,可以在IIR滤波器中使用更少的系数项来实现与FIR滤波器相近的滤波性能,如图16所示,用10阶IIR滤波器实现40阶FIR滤波器性能。从计算的角度来看,这使得IIR滤波器比FIR滤波器计算更快。如果一个滤波器必须实时应用(例如在听音时进行交互滤波),则通常使用IIR滤波器。然后,IIR滤波器也有一些自身的缺点:
延迟:IIR滤波器在不同频率处延迟不同,而FIR滤波器在每个频率处具有一致的延迟。
稳定性:由于其结构,IIR滤波器有时可能不稳定,无法计算或应用于数据。FIR滤波器始终稳定。
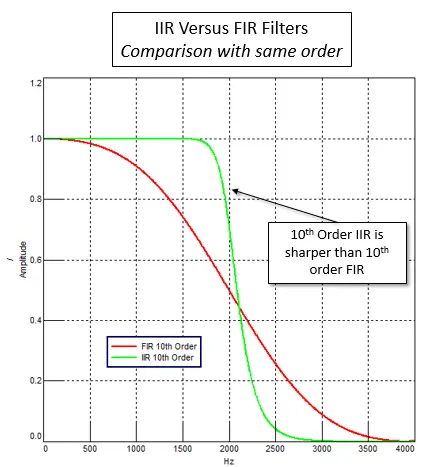
图15 相同阶数下,IIR滤波器比FIR滤波器具有更陡峭的衰减斜率
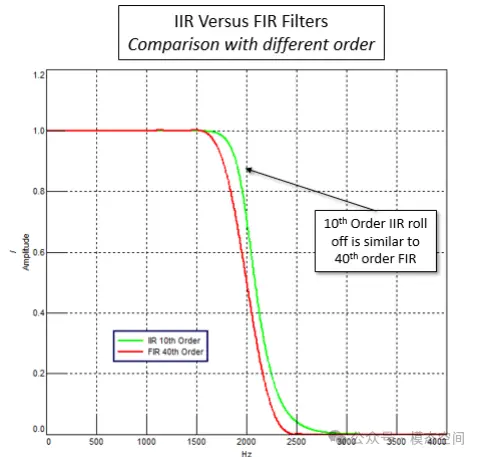
图16 更低阶的IIR滤波器可实现与FIR滤波器相似的特性
通常,我们希望设计一个具有与特定模拟滤波器特性等效的数字滤波器,因为大多数滤波器理论都是在模拟时代发展起来的。然而,这样精确的等效是不存在的,因此数字滤波器学科在很大程度上涉及如何使数字滤波器在某些方面最接近模拟滤波器的特性。在这里,涉及一些用户必须清楚的关于数字滤波器性能的基本事实。
重要的是要知道,越接近奈奎斯特频率,数字滤波器近似模拟滤波器的性能越来越差。因此,如果滤波器的特性是在模拟信号的频域定义的,如倍频程滤波器和人体振动计权滤波器,那么,在滤波信号之前应该使用足够高的过采样率。例如,在欧标IEC 61260(1995)和美标ANSI S1.11(2004)的倍频程滤波器标准中,建议最小过采样率为最高中心频率的5倍。一般情况下,在对数据进行数字滤波时,建议至少使用10倍过采样。
滤波器的一个重要问题是时间延迟。对于FIR滤波器而言,只计算输入信号,但是在滤波器工作之前,来自输入信号的许多时间数据样本必须通过与滤波项数(Nb)成比例的滤波器。直到通过滤波器的样本点数(n)大于Nb,滤滤后才开始计算第n个输出数据。由于某些数据必须通过滤波器后才能计算输出,因此与输入时间相比,会在输出中产生时间延迟。并且滤波器阶数越高,延迟更久。FIR和IIR滤波器的延迟特性非常不同,如图17所示,FIR滤波器在所有频率处有相同的时间延迟,而IIR滤波器的时间延迟随频率变化。
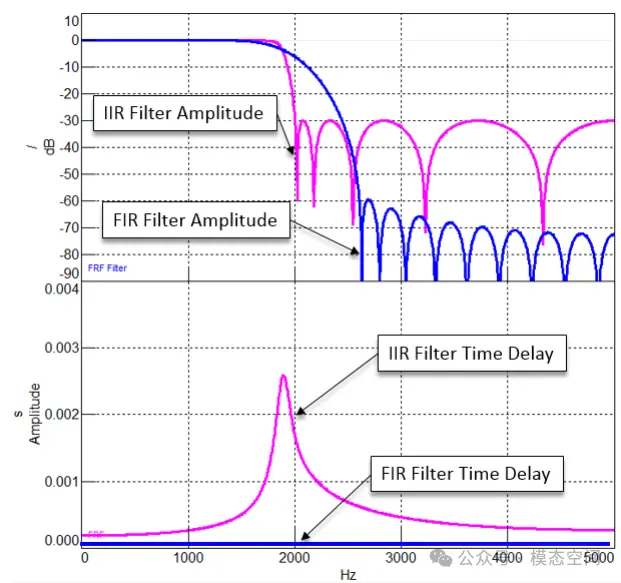
图17 IIR和FIR滤波器的幅频(上)和时间延迟(下)
来源:模态空间
作者:谭祥军












