横摆角速度、质心侧偏角以及车轮滑转率对车辆的转向稳定性都有着重要影响,因此需要综合考虑这三者共同作为转向稳定性控制策略的控制变量,以保证车辆的稳定安全运行。
车辆转向稳定性控制策略总体结构如图1所示,稳定性控制策略总体方案如图2所示。从图中可以看出该转向稳定性控制策略主要是三个子控制器构成:失稳判断模块、上层控制器、下层控制器。各个子控制器在完成自身控制器任务的同时也为其它控制器提供相应的信息。
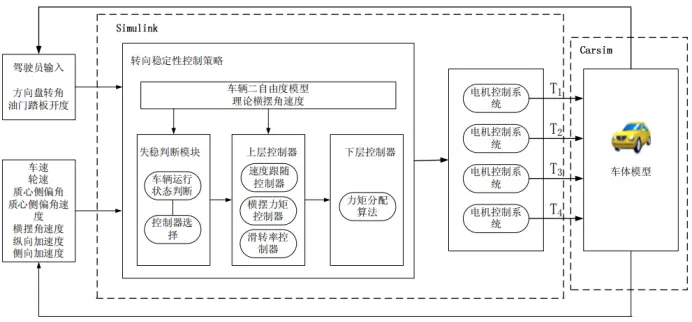
图1 转向稳定性控制策略总体结构图
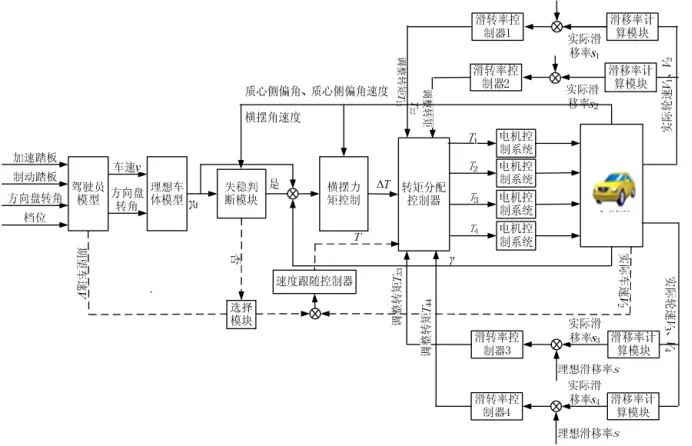
图2 转向稳定性控制策略总体方案图
从图中可以看出,该转向稳定性控制策略的工作模式如下所述:①首先根据驾驶员操作确定车辆的车速和方向盘转角,得到期望和实际的横摆角速度以及质心侧偏角和质心侧偏角速度;②失稳判断模块根据期望和实际的横摆角速度以及质心侧偏角和质心侧偏角速度判断车辆是否失稳;③若车辆不失稳,则以实际车速和期望车速的差值经过速度跟随控制器得到车辆所需的驱动力矩,并通过转矩分配控制器将驱动力矩平均分配给各车轮,保证车辆对期望车速的跟随性;④若车辆出现失稳情况,则横摆力矩控制器开始工作,该控制器以期望和实际的横摆角速度,经过PID控制得到使车辆恢复稳定运行所需的调整横摆力矩;⑤各车轮的滑转率判断各车轮滑转率是否超过给定值,若超过则相应的滑转率控制器开始工作,滑转率控制器以各车轮的实际滑转率和理想滑转率的偏差作为输入量,通过PID控制得到各个车轮的调整力矩;⑥得到的调整横摆力矩和各个车轮的调整力矩共同输入到转矩分配控制器中,转矩分配控制器根据合适的分配方法将这些调整力矩转化为各车轮上的驱动力或制动力矩,从而对车辆进行稳定性控制。
(1)速度跟随控制器保证车辆动力性,对目标车速进行跟踪控制,控制方法如下所示:
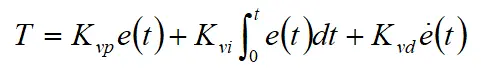
其中,速度跟随误差为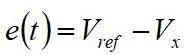 。Vref和Vx分别为目标速度和实际车速。
。Vref和Vx分别为目标速度和实际车速。
(2)当实际滑移率超过0.3时滑转率控制器开始工作,滑转率控制器如下所示:
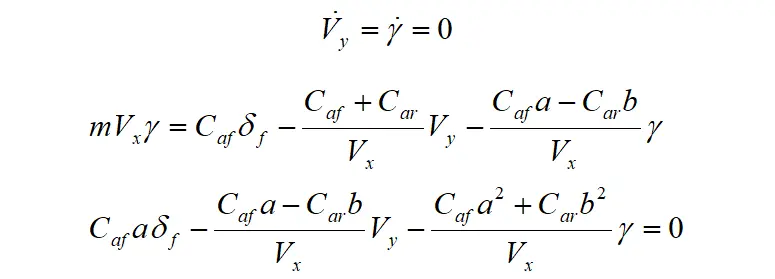
其中,滑转率跟随误差为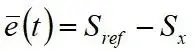 。Sref和Sx分别为理想滑转率和实际滑转率,低附着系数路面时的理想滑转率为0.05,高附着系数路面时的理想滑转率为0.15。
。Sref和Sx分别为理想滑转率和实际滑转率,低附着系数路面时的理想滑转率为0.05,高附着系数路面时的理想滑转率为0.15。
(3)横摆力矩控制器
横摆力矩控制器是车辆稳定性控制的核心之一,它通过期望横摆角速度和质心侧偏角同实际横摆角速度和质心侧偏角的偏差得到车辆的调整横摆力矩,PID控制算法如下所示:
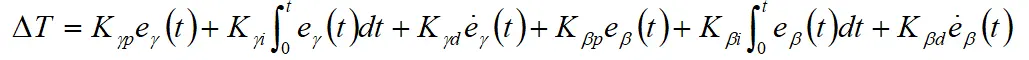
其中,横摆角速度跟随误差为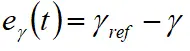 ,质心侧偏角跟随误差为
,质心侧偏角跟随误差为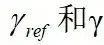 。
。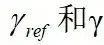 分别为目标横摆角速度和实际横摆角速度,
分别为目标横摆角速度和实际横摆角速度,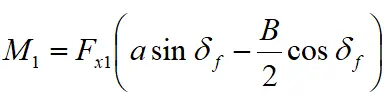 分别为目标质心侧偏角和实际质心侧偏角。目标横摆角速度和质心侧偏角可根据车辆二自由度模型的稳态转向特性计算,车辆二自由度模型为:
分别为目标质心侧偏角和实际质心侧偏角。目标横摆角速度和质心侧偏角可根据车辆二自由度模型的稳态转向特性计算,车辆二自由度模型为:
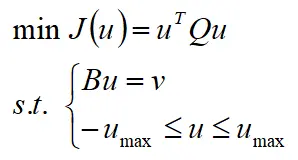
当车辆稳态行驶时,车辆的稳定行驶状态即为车辆二自由度模型的平衡点即
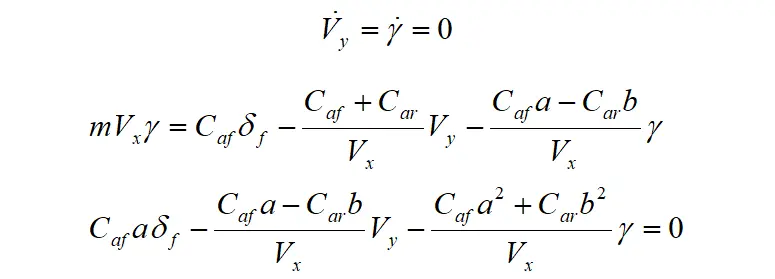
计算可得
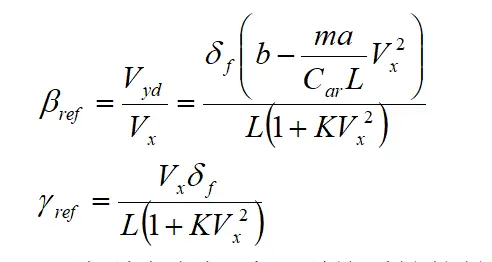
其中,m为整车质量,a、b分别为车辆质心到前后轴的轴距,L=a+b为前后轴距,Caf和Car分别为前后轮的侧偏刚度,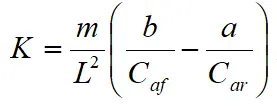 为不足转向系数。
为不足转向系数。
接下来,将重点介绍如何根据得到的调整横摆力矩和各个车轮的调整力矩转化为各车轮上的驱动力或制动力矩,主要包括三种常用的控制方法。
平均分配
平均分配方式是在车辆行驶过程中始终将驱动力和调整力矩平均分配给各个驱动车轮,分配公式如下所示。
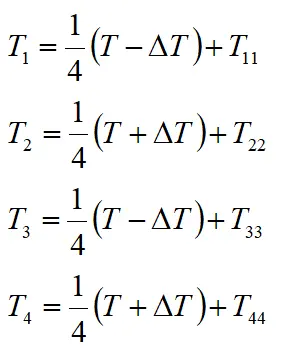
式中,Ti(i=1,2,3,4)分别表示左前轮、右前轮、左后轮、右后轮的驱动力力矩;T表示由速度跟随控制器得到的总驱动力矩,ΔT表示由横摆力矩控制器得到的调整横摆力矩,Tii(i=1,2,3,4)分别表示由四个滑转率控制器得到的四个车轮的调整力矩。
动态载荷分配
在车辆实际运行过程尤其是转向过程中,由于纵向加速度和侧向加速度的存在,导致车辆的垂直载荷发生了转移,各车轮所受的垂直载荷并不相等,由于车轮的最大附着力与路面附着系数和车轮所受垂直载荷有关,假设四个车轮的路面附着系数一定时,对于所受垂直载荷越大的车轮,路面所能提供的最大附着力也越大,车轮的附着能力越强,因此在对各车轮的驱动力矩进行分配时,需要考虑到轴荷转移对车轮附着能力的影响,附着能力大的车轮分配的驱动力矩应较大,附着能力小的车轮分配的驱动力矩应较小,这样能够更好的利用各车轮的附着能力,有效的防止车轮出现打滑,影响车辆的稳定性。
动态载荷分配方式即是在车辆行驶过程中,按照各个车轮的动态垂直载荷比例将驱动力和调整力矩分配给各个车轮,其中,各个车轮垂直载荷的变化如下所示
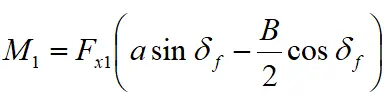
其中,B为前后轴轮距,ax、ay分别为车辆纵向与侧向加速度,hg为车辆重心高度,Fzi(i=1、2、3、4)为各个车轮的垂直载荷。则各车轮力和调整力矩的分配比例可以用下式表示
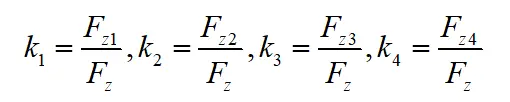
式中,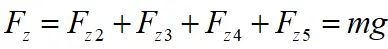 ,为车轮所受总的垂直载荷,
,为车轮所受总的垂直载荷,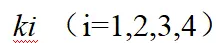 分别表示左前轮、右前轮、左后轮、右后轮的分配比例。则动态载荷的分配公式如下所示。
分别表示左前轮、右前轮、左后轮、右后轮的分配比例。则动态载荷的分配公式如下所示。
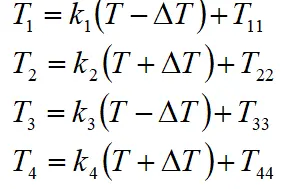
轮胎利用率最优分配
轮胎利用率最优分配是在考虑轴荷转移、电机输出限制、路面附着条件三个因素下的一种集成化的力矩分配方式。
在实际车辆控制过程中,横摆力矩不能过大,也不能过小,过大会引起车辆的过度转向,过小会引起车辆的不足转向;以车辆左转为例分析各车轮所受纵向力对横摆力矩的影响,左转时各车轮受力如下图所示。
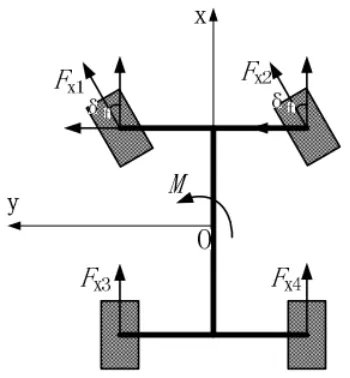
图3 转向受力示意图
车辆左前轮纵向力对质心O形成的横摆力矩可以由下式表示。
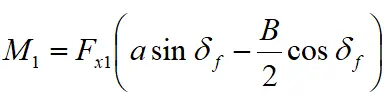
其中,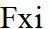 为车轮纵向力,
为车轮纵向力,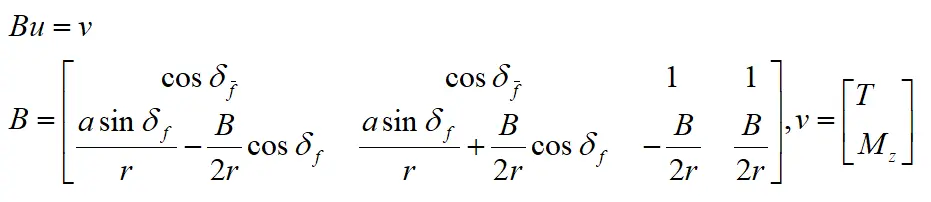 为前轮转角。
为前轮转角。
本文主要考虑纵向力的变化对车辆转向稳定性的影响,由图3可知,车辆所受总的纵向力与总的横摆力矩可以简化为
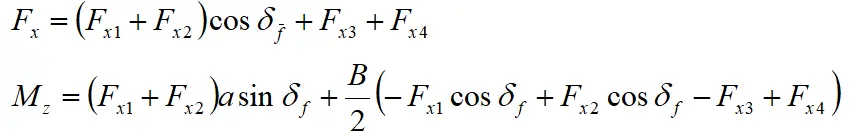
当车辆出现失稳,可以通过调整各车轮力矩使车辆的横摆力矩发生改变从而对车辆的运行状态进行调整。对车轮力矩进行调节时可以只调节某个车轮或某几个车轮的力矩,但这种调节方法容易对车辆的动力性造成影响,同时由于电机输出力矩和路面附着条件的限制,产生的调整横摆力矩也很有限,因此,在对车辆进行控制的同时对四个车轮的力矩进行调节,这样既能保证车辆动力性的要求,也能是车辆保持较高的调整横摆力矩裕度。根据以上分析,当前轮转角较小时,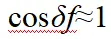 ,结合图3,以车辆向左不足转向为例,得到可行的车轮纵向力分配方法如下表所示。
,结合图3,以车辆向左不足转向为例,得到可行的车轮纵向力分配方法如下表所示。
表1 车轮纵向力力分配表

由于总的纵向驱动力矩T和横摆力矩Mz已知,可定义控制输入为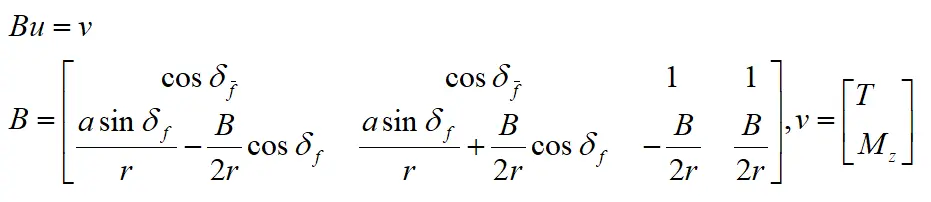 ,则输入u满足等式约束
,则输入u满足等式约束
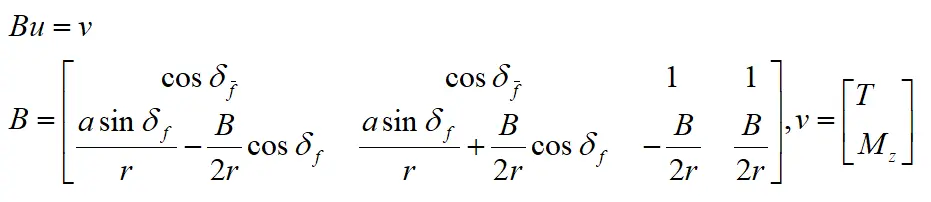
其中,r表示轮胎半径。
采用二次规划法对各车轮的驱动力进行求解,首先要明确目标函数和约束条件。在此引入轮胎利用率的概念,所谓轮胎利用率即是指单个车轮上的路面附着力与其所能获得的最大附着力之比,即
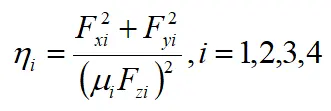
轮胎利用率可用来表示车辆的稳定性裕度,轮胎利用率越高表示车辆的稳定性裕度越低,当车辆轮胎利用率达到1时,轮胎已经达到附着能力的极限,车辆处于失稳的边缘。因此为了使车辆处于稳定工况,应尽可能的控制轮胎利用率,使其处于较低的水平。本文以所有轮胎利用率平方和最小为目标函数对各轮胎受力进行分配,保证各车轮均能保持稳定并且拥有一定的稳定裕度,以保证车辆的稳定运行。以四个轮胎利用率平方和最小为目标函数
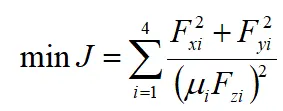
由于本文只考虑优化纵向力分配来提高车辆的稳定性,故可将目标函数简化为:
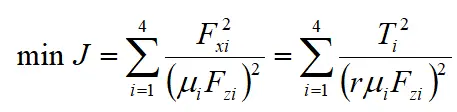
可写成
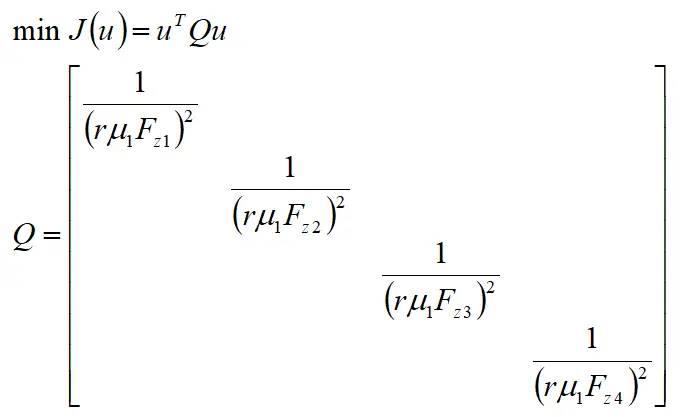
目标函数的约束条件包括电机输出限制和路面附着条件限制:
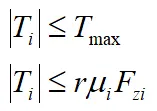
即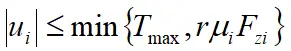 。则轮胎利用率最优二次分配模型为
。则轮胎利用率最优二次分配模型为
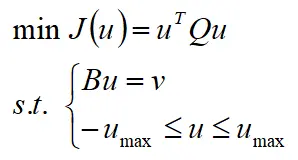
对比上述三种方法可见,前两种方法属于一种简单的rule-based,易实现,第三种方法属于optimization-based,可以获得较好的分配效果。
来源:智能运载装备研究所






